Exercise 1.4: Entropy Approximations for the AMI Code
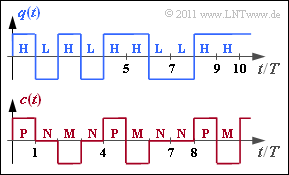
The graph above shows the binary source signal $q(t)$, which can also be described by the symbol sequence $\langle q_\nu \rangle$ with $q_\nu \in \{ {\rm L}, {\rm H} \}$ . In the entire task, $p_{\rm L} = p_{\rm H} =0.5$ applies.
The coded signal $c(t)$ and the corresponding symbol sequence $\langle c_\nu \rangle$ with $c_\nu \in \{{\rm P}, {\rm N}, {\rm M} \}$ results from the AMI coding ("Alternate Mark Inversion") according to the following rule:
- The binary symbol $\rm L$ ⇒ "Low"is always represented by the ternary symbol $\rm N$ ⇒ "German: Null" ⇒ "Zero".
- The binary symbol $\rm H$ ⇒ "High" is also encoded deterministically but alternately (hence the name "Alternate Mark Inversion") by the symbols $\rm P$ ⇒ "Plus" and $\rm M$ ⇒ "Minus".
In this task, the entropy approximations for the AMI coded signal are to be calculated:
- Approximation $H_1$ refers only to the symbol probabilities $p_{\rm P}$, $p_{\rm N}$ and $p_{\rm M}$.
- The $k$–th is the entropy approximation $(k = 2, 3, \text{...} \ )$ can be determined according to the following equation:
- $$H_k = \frac{1}{k} \cdot \sum_{i=1}^{3^k} p_i^{(k)} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p_i^{(k)}} \hspace{0.5cm}({\rm Einheit\hspace{-0.1cm}: \hspace{0.1cm}bit/Symbol}) \hspace{0.05cm}.$$
- Here, $p_i^{(k)}$ the $i$–th composite probability of a $k$–tuple.
Hints:
- This task belongs to the chapter Discrete Sources with Memory.
- Reference is made in particular to the page The Entropy of the AMI code.
- In Exercise 1.4Z the actual entropy of the encoded sequence $\langle c_\nu \rangle$ is calculated to $H = 1 \; \rm bit/symbol$.
- The following relations between the units are to be expected: $H \le$ ...$ \le H_3 \le H_2 \le H_1 \le H_0 \hspace{0.05cm}.$
Questions
Solution
- $$H_0 = {\rm log}_2\hspace{0.1cm} M = {\rm log}_2\hspace{0.1cm} (3) \hspace{0.15cm} \underline { = 1.585 \,{\rm bit/symbol}} \hspace{0.05cm}.$$
(2) The first-order entropy approximation takes into account only the symbol probabilities $p_{\rm P}$, $p_{\rm N}$ and $p_{\rm M}$
and not the statistical bindings within the code sequence $\langle c_\nu \rangle$. Thus one obtains:
- $$p_{\rm N} = p_{\rm L} = 1/2\hspace{0.05cm},\hspace{0.2cm}p_{\rm P} = p_{\rm M} = p_{\rm H}/2 = 1/4 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} H_1 = \frac{1}{2} \cdot {\rm log}_2\hspace{0.1cm} (2) + 2 \cdot \frac{1}{4} \cdot {\rm log}_2\hspace{0.1cm}(4) \hspace{0.15cm} \underline {= 1.5 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$
(3) First, the $M^2 = 9$ composite probabilities of two-tuples have to be determined here, in the following marked by the first two code symbols $c_1$ and $c_2$:
- Since in the AMI code neither $\rm P$ can follow $\rm P$ nor $\rm M$ can follow $\rm M$ , $p_{\rm PP} = p_{\rm MM} =0$.
- For the composite probabilities under the condition $c_2 = \rm N$ applies:
- $$p_{\rm NN} \hspace{0.1cm} = \hspace{0.1cm} {\rm Pr}( c_1 = \mathbf{N}) \cdot {\rm Pr}(c_2 = \mathbf{N}\hspace{0.05cm} | c_1 = \mathbf{N}) = 1/2 \cdot 1/2 = 1/4 \hspace{0.05cm},$$
- $$ p_{\rm MN} \hspace{0.1cm} = \hspace{0.1cm} {\rm Pr}( c_1 = \mathbf{M}) \cdot {\rm Pr}(c_2 = \mathbf{N}\hspace{0.05cm} | c_1 = \mathbf{M}) = 1/4 \cdot 1/2 = 1/8 \hspace{0.05cm},$$
- $$ p_{\rm PN} \hspace{0.1cm} = \hspace{0.1cm} {\rm Pr}( c_1 = \mathbf{P}) \cdot {\rm Pr}(c_2 = \mathbf{N}\hspace{0.05cm} | c_1 = \mathbf{P}) = 1/4 \cdot 1/2 = 1/8 \hspace{0.05cm}.$$
- The composite probabilities of the two-tuples $\rm PM$ and $\rm MP$ are:
- $$p_{\rm PM} \hspace{0.1cm} = \hspace{0.1cm} {\rm Pr}( c_1 = \mathbf{P}) \cdot {\rm Pr}(c_2 = \mathbf{M}\hspace{0.05cm} | c_1 = \mathbf{P}) = 1/4 \cdot 1/2 = 1/8 \hspace{0.05cm},$$
- $$ p_{\rm MP} \hspace{0.1cm} = \hspace{0.1cm} {\rm Pr}( c_1 = \mathbf{M}) \cdot {\rm Pr}(c_2 = \mathbf{P}\hspace{0.05cm} | c_1 = \mathbf{M}) = 1/4 \cdot 1/2 = 1/8 \hspace{0.05cm}.$$
- For the remaining probabilities, it must also be taken into account whether the binary symbol $\rm H$ was encoded with $\rm P$ or with $\rm M$ last time ⇒ further factor $1/2$:
- $$p_{\rm NM} \hspace{0.1cm} = \hspace{0.1cm} {\rm Pr}( c_1 = \mathbf{N}) \cdot {\rm Pr}(c_2 = \mathbf{M}\hspace{0.05cm} | c_1 = \mathbf{N}) = 1/2 \cdot 1/2 \cdot 1/2= 1/8 \hspace{0.05cm},$$
- $$ p_{\rm NP} \hspace{0.1cm} = \hspace{0.1cm} {\rm Pr}( c_1 = \mathbf{N}) \cdot {\rm Pr}(c_2 = \mathbf{P}\hspace{0.05cm} | c_1 = \mathbf{N}) = 1/2 \cdot 1/2 \cdot 1/2 = 1/8 \hspace{0.05cm}.$$
Thus the entropy $H_2'$ of a two-tuple or its entropy $H_2$ per code symbol:
- $$H_2\hspace{0.01cm}' = \frac{1}{4} \cdot {\rm log}_2\hspace{0.1cm} (4) + 6 \cdot \frac{1}{8} \cdot {\rm log}_2\hspace{0.1cm}(8) \hspace{0.15cm} {= 2.75 \,{\text{bit/two-tuple} }}\hspace{0.3cm} \Rightarrow\hspace{0.3cm} H_2 = \frac{H_2\hspace{0.01cm}'}{2} \hspace{0.15cm} \underline {= 1.375 \,{\rm bit/symbol}} \hspace{0.05cm}.$$
(4) The calculation of $H_3$ is similar to the last subtask for $H_2$, except that now $3^3 = 27$ composite probabilities must be determined:
- $$p_{\rm NNN} = 1/8\hspace{0.4cm}{\rm (nur \hspace{0.15cm}only once)} \hspace{0.05cm},$$
- $$p_{\rm NMM} = p_{\rm NPP} = p_{\rm MNM} = ... = 0 \hspace{0.4cm}{\rm (total \hspace{0.15cm}12)} \hspace{0.05cm},$$
- $$p_{\rm NNM} = p_{\rm NNP} = p_{\rm PMP} = ... = 1/16 \hspace{0.4cm}{\rm (total \hspace{0.15cm}14)}$$
- $$\Rightarrow\hspace{0.3cm} H_3 = \frac{1}{3} \cdot \left [ \frac{1}{8} \cdot {\rm log}_2\hspace{0.1cm} (8) + 14 \cdot \frac{1}{16} \cdot {\rm log}_2\hspace{0.1cm}(16) \right ] \hspace{0.15cm} \underline {= 1.292 \,{\rm bit/symbol}} \hspace{0.05cm}.$$
(5) Correct are the proposed solutions 1 and 2.
- On the other hand, statement 3 is wrong, because $H_4$ must in any case be smaller than $H_3 = 1.292 \; \rm bit/symbol$.