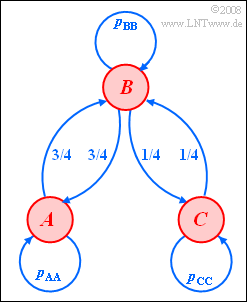
We consider a Markov chain with three possible events $A$, $B$, $C$:
- The transition probabilities are shown in the graph.
- Thus, a transition from $A$ to $C$ and vice versa is not possible.
- $$p_\text{AC} = p_\text{CA} = 0.$$
The three event probabilities at the starting time $(\nu = 0)$ are given as follows:
- $${\rm Pr}(A_0) = 0,$$
- $${\rm Pr}(B_0) = 1,$$
- $${\rm Pr}(C_0) = 0.$$
Hints:
- The exercise belongs to the chapter Markov Chains.
- In particular, reference is made to the page Matrix vector representation.
Questions
Solution
(1) In general (or in this special case) it must hold:
- $$p_{\rm AA} = 1 - p_{\rm AB} - p_{\rm AC} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} p_{\rm AA} = 1 - 0.75 -0 \hspace{0.15cm}\underline {= 0.25},$$
- $$p_{\rm BB} = 1 - p_{\rm BA} - p_{\rm BC} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} p_{\rm BB} = 1 - 0.75 -0.25 \hspace{0.15cm}\underline {= 0},$$
- $$p_{\rm CC} = 1 - p_{\rm CA} - p_{\rm CB} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} p_{\rm CC} = 1 - 0 - 0.25 \hspace{0.15cm}\underline {= 0.75}.$$
- Thus, the transition matrix is:
- $${\mathbf{P}} = \left[ \begin{array}{ccc} 1/4 & 3/4 & 0 \\ 3/4 & 0 & 1/4 \\ 0 & 1/4 & 3/4 \end{array} \right] .$$
(2) Because of ${\rm Pr}(B_0) = 1$ and $p_\text{BB} = 0$, at time $\nu = 1$ the event $B$ cannot occur and $A$ is much more probable than $C$:
- $$\hspace{0.15cm}\underline {{\rm Pr}(A_1) = 0.75}; \hspace{0.5cm} {\rm Pr}(B_1) = 0; \hspace{0.5cm}{\rm Pr}(C_1) = 0.25.$$
- The same result is obtained by applying the vector matrix representation.
(3) For the probability vector at time $\nu = 2$ holds:
- $${\mathbf{p}^{(\nu = 2)}} = {\mathbf{P}}^{\rm T} \cdot {\mathbf{p}^{(\nu =1 )}}= \left[ \begin{array}{ccc} 1/4 & 3/4& 0 \\ 3/4 & 0 & 1/4 \\ 0& 1/4& 3/4 \end{array} \right] \left[ \begin{array}{c} 3/4 \\ 0 \\ 1/4 \end{array} \right] = \left[ \begin{array}{c} 3/16 \\ 10/16 \\ 3/16 \end{array} \right] .$$
- Thus, the event probability is ${\rm Pr}(A_2) = 3/16\hspace{0.15cm}\underline {= 0.1875}$.
(4) To solve this problem, several possibilities should be given.
- One is to solve a system of equations with three unknowns:
- $${\rm Pr}(A) = 1/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(A) \hspace{0.1cm} + \hspace{0.1cm} 3/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(B),$$
- $${\rm Pr}(B) = 3/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(A) \hspace{2.8cm} + \hspace{0.1cm} 1/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(C),$$
- $${\rm Pr}(C) = \hspace{2.8cm} 1/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(B) \hspace{0.1cm} + \hspace{0.1cm} 3/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(C).$$
- From the first equation we get ${\rm Pr}(B) = {\rm Pr}(A)$, from the last ${\rm Pr}(C) = {\rm Pr}(A)$. Since the sum of all probabilities is equal to $1$, it follows
- $$ {\rm Pr}(A) = {\rm Pr}(B) = {\rm Pr}(C) = 1/3 \hspace{0.15cm}\underline {\approx 0.333}.$$
- The same result is obtained by analyzing the transition matrix. Since the sum of each column equals $1$ $($that is, the sum of each row of the transposed matrix also equals $1)$, it is obvious that all event probabilities must be equal.
- Even by thinking about it briefly, one could have predicted the result without calculating. Since at each event the numerical values at the outgoing arrows (only to other events) are equal with those at the incoming ones, it is not to be seen why one of the events should be preferred.