Exercise 2.12: Decoding at RSC (7, 4, 4) to Base 8

ELP assignment schemes for $r = 1, \ r = 2, \ r = 3$

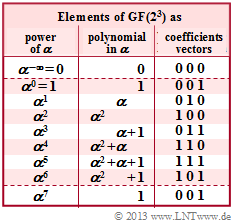
We analyze the Peterson algorithm detailed in the section "Procedure for Bounded Distance Decoding". Assumed is the Reed–Solomon code with parameters $n = 7, \ k = 4$ and $d_{\rm min} = 4$, where all code symbols come from $\rm GF(2^3)$ and all arithmetic operations are consequently to be performed in $\rm GF(2^3)$ as well.

The parity-check matrix of this code is:

$${ \boldsymbol{\rm H}} = \begin{pmatrix} 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5}\\ 1 & \alpha^3 & \alpha^6 & \alpha^2 & \alpha^{5} & \alpha^{1} & \alpha^{4} \end{pmatrix} \hspace{0.05cm}.$$

In "Step $\rm (A)$" of the decoding algorithm considered here, the syndrome $\underline{s} = \underline{y} \cdot \mathbf{H}^{\rm T}$ must be computed.
For the received word $\underline{y} = (\alpha^1, \, 0, \, \alpha^3, \, 0, \, 1, \, \alpha, \, 0)$, the syndrome results in $\underline{s} = (\alpha^4, \, \alpha^5, \, \alpha^6)$, as in the Exercise 2.12Z yet to be shown.
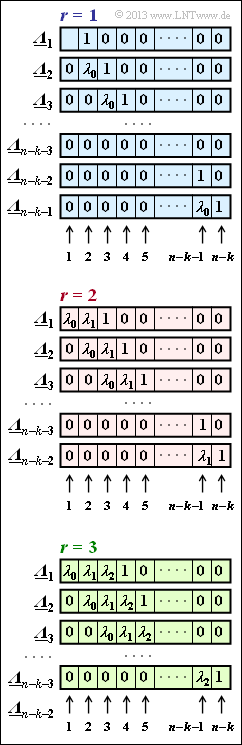
After that the "ELP coefficient vectors" be set up and evaluated according to the adjacent figure, where the assignment depends on whether one assumes $r = 1, \ r = 2$ or $r = 3$ symbol errors in the received word.
If all equations ${\it \underline{\Lambda}}_l \cdot \underline{s}^{\rm T} = 0$ are satisfied for the assumed symbol error count $r$, then the received word $\underline{y}$ actually has exactly $r$ symbol errors.

Hints:

The exercise refers to the chapter "Error correction according to Reed–Solomon coding".

"ELP" stands for "Error Locator Polynomial".

You can take the further steps from the theory part:

Step $\rm (C)$: "Localization of error locations",
Step $\rm (D)$: "Determination of the error values".

Questions

Solution

(1) Correct is the proposed solution 1:

The considered Reed–Solomon code $(7, \, 4, \, 4)_8$ can only correct $t = ⌊(d_{\rm min} - 1)/2⌋ = 1$ symbol errors because of $d_{\rm min} = 4$.

So only the scheme with blue background is relevant, which is valid for the case that there is exactly one symbol error in the received words $(r = 1)$.

(2) According to the graph on the specification page, the vector ${\it \underline{\Lambda}}_l$ here has $L = n - k \ \underline{= 3}$ elements.

(3) There are only the two ELP coefficient vectors ${\it \underline{\Lambda}}_1 = (\lambda_0, \, 1, \, 0)$, ${\it \underline{\Lambda}}_2 = (0, \, \lambda_0, \, 1) \ \Rightarrow \ l_{\rm max} \ \underline{= 2}$.

(4) From ${\it \underline{\Lambda}}_1$ and ${\it \underline{\Lambda}}_2$ we get two scalar equations of determination ⇒ ${\it \underline{\Lambda}}_l \cdot \underline{s}^{\rm T} = 0$ for the parameter $\lambda_0$:

$$\lambda_0 \cdot \alpha^4 + \alpha^5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 \cdot \alpha^4 = -\alpha^5 = \alpha^5 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha \hspace{0.05cm},$$

$$\lambda_0 \cdot \alpha^5 + \alpha^6 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha \hspace{0.05cm}.$$

The equation system is uniquely solvable ⇒ Answer YES.

(5) Using the result of subtask (4) ⇒ $\lambda_0 = \alpha$, we obtain for the error locator polynomial:

$${\it \Lambda}(x)=x \cdot \big ({\it \lambda}_0 + x \big ) =x \cdot \big (\alpha + x )$$

$$\Rightarrow \hspace{0.3cm} {\it \Lambda}(\alpha^0 )\hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1 \cdot \big ( \alpha + 1 \big ) = \alpha + 1 \ne 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm No\hspace{0.15cm} zeros}\hspace{0.05cm},$$

$$\hspace{0.875cm} {\it \Lambda}(\alpha^1)\hspace{-0.15cm} \ = \ \hspace{-0.15cm}\alpha \cdot \big (\alpha + \alpha\big ) = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{ \boldsymbol{\rm Zeros}}\hspace{0.05cm}.$$

So the symbol at position 1 was falsified ⇒ Solution suggestion 2.

Since the calculation in subtask (4) was done under the condition $r = 1$, all other symbols were transferred correctly:

$\rm GF(2^3)$ representation as powers, polynomials, vectors

$$\underline {e} = (0, e_1, 0, 0, 0, 0, 0)\hspace{0.05cm}. $$

(6) From the condition $\underline{e} \cdot \mathbf{H}^{\rm T} = \underline{s}^{\rm T}$ follows

$$(0, e_1, 0, 0, 0, 0, 0) \cdot \begin{pmatrix} 1 & 1 & 1 \\ \alpha^1 & \alpha^2 & \alpha^3 \\ \alpha^2 & \alpha^4 & \alpha^6 \\ \alpha^3 & \alpha^6 & \alpha^9 \\ \alpha^4 & \alpha^8 & \alpha^{12} \\ \alpha^5 & \alpha^{10} & \alpha^{15} \\ \alpha^6 & \alpha^{12} & \alpha^{18} \end{pmatrix} \hspace{0.15cm}\stackrel{!}{=} \hspace{0.15cm} \begin{pmatrix} \alpha^4\\ \alpha^5\\ \alpha^6 \end{pmatrix} $$

$$\Rightarrow \hspace{0.3cm} e_1 \cdot \alpha = \alpha^4\hspace{0.05cm},\hspace{0.4cm} e_1 \cdot \alpha^2 = \alpha^5\hspace{0.05cm},\hspace{0.4cm} e_1 \cdot \alpha^3 = \alpha^6\hspace{0.05cm}. $$

The solution always leads to the result $e_1 = \alpha^3$ ⇒ Answer 2.

With the received word $\underline{y} = (\alpha^1, \, 0, \, \alpha^3, \, 0, \, 1, \, \alpha^1, \, 0)$, the decoding result is $\underline{z} = (\alpha^1, \, \alpha^3, \, \alpha^3, \, 0, \, 1, \, \alpha^1, \, 0)$.

(7) Analogous to the subtask (4), the system of equations is now:

$$\lambda_0 \cdot \alpha^2 + \alpha^4 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha^2 \hspace{0.05cm},$$

$$\lambda_0 \cdot \alpha^4 + \alpha^5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha \hspace{0.05cm}.$$

The two solutions contradict each other. At least two symbols have been falsified during transmission. The decoding fails ⇒ Answer NO.

You would now have to start a new attempt according to the red scheme $(r = 2)$.

	The blue highlighted schema $(r = 1)$.
	The red highlighted schema $(r = 2)$.
	The green highlighted schema $(r = 3)$.

	YES.
	NO.

	The symbol "0",
	the symbol "1",
	the symbol "6".

	$e_i = \alpha^2$,
	$e_i = \alpha^3$,
	$e_i = 1$.

	YES.
	NO.