Exercise 2.13: Inverse Burrows-Wheeler Transformation

• Return to book

BWT result to be analyzed

The  "Burrows–Wheeler Transformation" – abbreviated  $\rm BWT$  – causes a blockwise sorting of the characters of a text with the aim of preparing the text for efficient data compression with the help of run-length coding or entropy coding.

• First, an  $N×N$ matrix is generated from a block of length  $N$,  with each row of this first matrix resulting from the preceding row by cyclic left shift.

• Then the matrix is sorted lexicographically  (without special characters:   alphabetically) .  The result of the BWT is the last row of the new BWT matrix, the so-called  $\text{L column}$  (from "Last").

• Further, this task refers to the  $\text{F column}$  (from "First", first row of the BWT matrix), which is needed for the inverse Burrows–Wheeler Transformation   ⇒   reconstruction of the original text from the L column.

• For the inverse BWT, the so-called  "primary index"  $I$  is also required.  This indicates the row of the BWT matrix in which the algorithm must be started.

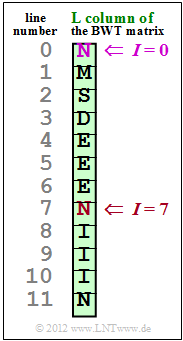
The graphic shows the result of a BWT, more precisely its L column.  The original text is to be reconstructed from this according to the description in the theory section  Burrows–Wheeler Transformation,

• in subtask  (2)  with the primary index  $I = 7$,
• in subtask  (3)    $I = 0$  is to be assumed.

Hints:

• The exercise belongs to the chapter  Further Source Coding Methods.
• In particular, reference is made to the section  Burrows–Wheeler Transformation.

Questions

1

What is the  $\text{F column}$ associated with the given  $\text{L column}$ ?

	$\rm SEINMEINDEIN$,
	$\rm NIIINEEEDSMN$,
	$\rm DEEEIIIMNNNS$.

2

What is the result of the reconstruction with primary index  $\underline{I = 7}$?

	$\rm MEINDEINSEIN$,
	$\rm DEINSEINMEIN$,
	$\rm NIESNIEDNIEM$.

3

What happens if the reconstruction  $\text{(inverse BWT transformation})$  starts from the wrong primary index  $I = 0$ ?

	$\rm MEINDEINSEIN$,
	$\rm DEINSEINMEIN$,
	$\rm NIESNIEDNIEM$.

4

Why is the Burrows–Wheeler transformation better suited than the original with regard to a later data compression?

	It results in more favourable character frequencies.
	All characters are sorted lexicographically.
	Identical characters follow each other more often in the BWT.

Solution

Solution

(1)  The solution suggestion 3 is correct:

• The first column of the BWT matrix is also called the  "F column"  and the last column the  "L column"  (from  "First"  or  "Last").
• Only the  "L column" is passed on to the next coding level.
• The  "F column", which is also needed for the reverse transformation, results from the  "L column"  by lexicographically sorting.

Inverse BWT with  $I = 7$  (left) or  $I = 0$  (right)

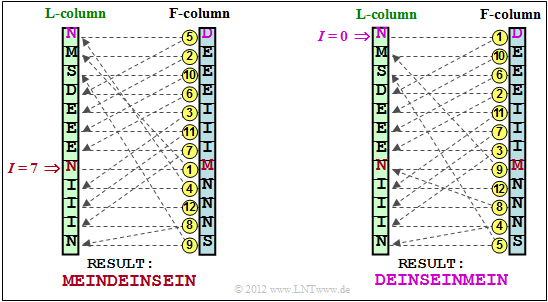
(2)  The solution suggestion 1 is correct:   MEINDEINSEIN, as can be seen from the left-hand representation of the following diagram.
Note that the top line represents the line number  $I = 0$  in each case. For explanation:

• Start the decoding with the line  $I = 7$  of the  "F column". 
  The content is  $\rm M$.
• Search for the corresponding  $\rm M$  in the  "L column"  and find it in line number  "1".
• From line 1 of the  "L column"  one goes horizontally to the  "F column"  and finds the symbol  $\rm E$.
• Similarly, one finds the third output symbol  $\rm I$  in line 4 of the  "F column".
• The decoding algorithm ends with the output symbol  $\rm N$  in the third last row.

(3)  Correct is the proposed solution 2:   $\rm DEINSEINMEIN$, as shown in the graph on the right.

(4)  Correct is the suggested solution 3:

• In BWT, four characters here are equal to their predecessors, in the original none.
• In the  "F column",  even more characters would be the same as their respective predecessors  (6 in total)  due to the lexicographical sorting, but this sorting cannot be reversed without loss.
• Solution suggestion 1 is wrong too:  
  The original and BWT contain exactly the same characters  $($three times  $\rm E$,  three times  $\rm I$,  three times  $\rm N$ and one each of  $\rm D$,  $\rm M$  and  $\rm S)$.