Exercise 2.3Z: Asymmetrical Characteristic Operation
The cosine signal
- $$x(t) = A \cdot \cos(\omega_0 t)$$
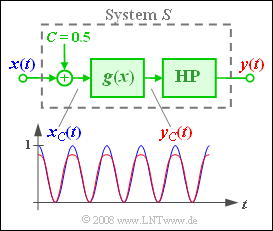
is applied to the input of a system $S$ where $A = 0.5$ shall always hold for the amplitude. The system $S$ consists of
- the addition of a direct (DC) component $C$,
- a nonlinearity with the characteristic curve
- $$g(x) = \sin(x) \hspace{0.05cm} \approx x -{x^3}\hspace{-0.1cm}/{6} = g_3(x),$$
- as well as an ideal high-pass filter that allows all frequencies to pass unaltered except for a direct (DC) signal $(f = 0)$.
The output signal of the overall system can generally be depicted as follows:
- $$y(t) = A_0 + A_1 \cdot \cos(\omega_0 t) + A_2 \cdot \cos(2\omega_0 t) + A_3 \cdot \cos(3\omega_0 t) + \hspace{0.05cm}\text{...}$$
The sinusoidal characteristic curve $g(x)$ is to be approximated by the cubic approximation $g_3(x)$ throughout the whole problem according to the above equation.
This would result in exactly the same constellation as in Exercise 2.3 for $C = 0$ in whose subtask (2) the distortion factor was calculated:
- $K = K_{g3} \approx 1.08 \%$ für $A = 0.5$,
- $K = K_{g3} \approx 4.76 \%$ für $A = 1.0$.
Considering the constants $A = C = 0.5$ the following holds for the input signal of the nonlinearity:
- $$x_{\rm C}(t) = C + A \cdot \cos(\omega_0 t) = {1}/{2} + {1}/{2}\cdot \cos(\omega_0 t).$$
- So, the characteristic curve is operated asymmetrically with values between $0$ and $1$.
- In the above graph, the signals $x_{\rm C}(t)$ and $y_{\rm C}(t)$ are plotted additionally directly before and after the characteristic curve $g(x)$ .
Please note:
- The exercise belongs to the chapter Nonlinear Distortions.
- The following trigonometric relations are assumed to be known:
- $$\cos^2(\alpha) = {1}/{2} + {1}/{2} \cdot \cos(2\alpha)\hspace{0.05cm}, \hspace{0.3cm} \cos^3(\alpha) = {3}/{4} \cdot \cos(\alpha) + {1}/{4} \cdot \cos(3\alpha) \hspace{0.05cm}.$$
Questions
Solution
- $$y_{\rm C}(t) = g_3\big[x_{\rm C}(t)\big] = \big[ C + A \cdot \cos(\omega_0 t)\big] - {1}/{6} \cdot \big[ C + A \cdot \cos(\omega_0 t)\big]^3 $$
- $$\Rightarrow \; y_{\rm C}(t) = C + A \cdot \cos(\omega_0 t) - {1}/{6} \cdot \big[ C^3 + 3 \cdot C^2 \cdot A \cdot \cos(\omega_0 t) + \hspace{0.09cm}3 \cdot C \cdot A^2 \cdot \cos^2(\omega_0 t) + A^3 \cdot \cos^3(\omega_0 t)\big].$$
- The signal $y_{\rm C}(t)$ contains a direct (DC) component $C - C^3/6$ which is no longer included in the signal $y(t)$ due to the high-pass filter:
- $$\underline{ A_0 = 0}.$$
(2) Applying the given trigonometric relations the following coefficients with $A= C = 0.5$ are obtained:
- $$A_1 = A - {1}/{6}\cdot 3 \cdot C^2 \cdot A - {1}/{6} \cdot {3}/{4}\cdot A^3 = {1}/{2} - {1}/{16} - {1}/{64} = {27}/{64} \hspace{0.15cm}\underline{ \approx 0.422},$$
- $$A_2 = - {1}/{6}\cdot 3 \cdot {1}/{2}\cdot C \cdot A^2 = - \frac{1}{32} \hspace{0.15cm}\underline{\approx -0.031},$$
- $$A_3 = - {1}/{6}\cdot \frac{1}{4}\cdot A^3 = - {1}/{192} \hspace{0.15cm}\underline{\approx -0.005}.$$
- Higher order terms do not occur. Thus, $\underline{A_4 = 0}$ holds.
(3) In this task, the higher order distortion factors are $K_2 = 2/27 \approx 7.41\%$ and $K_3 = 1/81 \approx 1.23\%$.
- Thereby, the following is obtained for the overall distortion factor:
- $$K = \sqrt{K_2^2 + K_3^2} \hspace{0.15cm}\underline{\approx7.51 \%}.$$
(4) The maximum value occurs at time $t = 0$ and at multiples of $T$ :
- $$y_{\rm max}= y(t=0) = A_1 + A_2 + A_3 = 0.422 -0.031 -0.005 \hspace{0.15cm}\underline{= 0.386}.$$
- The minimum values are located exactly in the middle between two maxima and it holds that:
- $$y_{\rm min}= - A_1 + A_2 - A_3 = -0.422 -0.031 +0.005\hspace{0.15cm}\underline{ = -0.448}.$$
- The signal $y(t)$ is shifted downward by $0.448$ compared to the signal drawn in the sketch on the information page.
- This signal value is obtained from the following equation considering $A = C = 1/2$:
- $$C - \frac{C \cdot A^2}{4}- \frac{C^3}{6} = {1}/{2} - {1}/{32}- {1}/{48} = 0.448.$$