Exercise 3.6: Transversal Filter of the Optimal Nyquist Equalizer

Transversal filter of the
Optimal Nyquist Equalizer

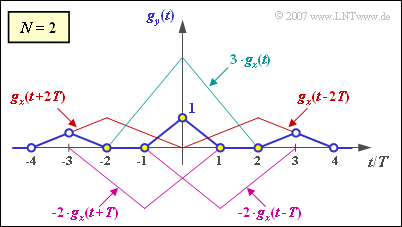
At the input of the symmetric second order transversal filter $(N = 2)$ shown in the diagram there is a triangular pulse $($normalized to $1)$:

$$g_x(t) = \left\{ \begin{array}{c} 1 - {|\hspace{0.05cm}t\hspace{0.05cm}|}/{(2T)} \\ \\ 0 \\ \end{array} \right. \begin{array}{*{1}c} {\rm{for}}\\ \\ {\rm{for}} \\ \end{array} \begin{array}{*{20}c}|\hspace{0.05cm}t\hspace{0.05cm}| \le 2\hspace{0.05cm}T, \\ \\ |\hspace{0.05cm}t\hspace{0.05cm}| \ge 2\hspace{0.05cm}T. \\ \end{array}$$

If all filter coefficients $k_0$, $k_1$ and $k_2$ are nonzero, then the following holds for the pulse at the output:

$$g_y(t) \ = k_0 \cdot g_x(t) + k_1 \cdot \big[ g_x(t-T)+ g_x(t+T) \big] + k_2 \cdot \big[ g_x(t-2T)+ g_x(t+2T) \big]\hspace{0.05cm}.$$

By appropriate choice of filter coefficients $k_0$, $k_1$ and $k_2$, the output pulse can satisfy the following conditions:

$$g_0 = g_y(t = 0) = 1,\hspace{0.2cm}g_1 = g_y(t = \pm T) = 0,\hspace{0.2cm}g_2 = g_y(t = \pm 2 T) = 0 \hspace{0.05cm}.$$

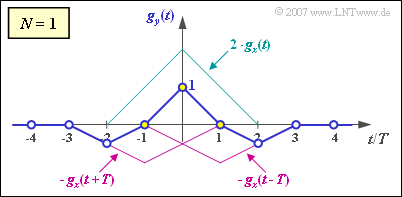
A first order filter $(N = 1)$ is obtained from the above arrangement and equation by setting the coefficient $k_2 = 0$.

Then, by appropriate choice of $k_0$ and $k_1$, $g_0 = 1$ and $g_1 = 0$ can be obtained. However, in this case, always will be $g_2 ≠ 0$.

Note: The exercise belongs to the chapter "Linear Nyquist Equalization".

Questions

$k_0\ = \ $

$k_1\ = \ $

$g_2\ = \ $

$g_3\ = \ $

$k_0\ = \ $

$k_1\ = \ $

$k_2\ = \ $

$g_3\ = \ $

$g_4\ = \ $

Solution

(1) The input pulse $g_x(t)$ is given by the following samples at multiples of $T$:

$$g_x(t = 0) = 1,\hspace{0.2cm}g_x(t = \pm T) = 0.5,\hspace{0.2cm}g_x(t = \pm 2 T) = ... = 0 \hspace{0.05cm}.$$

Thus, the following system of equations can be set up:

Output pulse for $N = 1$

$$t = 0\hspace{-0.1cm}:\hspace{0.2cm}g_0 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} k_0 \cdot 1.0 + k_1 \cdot 2 \cdot 0.5 = 1\hspace{0.05cm},$$

$$t = T\hspace{-0.1cm}:\hspace{0.2cm}g_1 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} k_0 \cdot 0.5 + k_1 \cdot 1.0 = 0 \hspace{0.05cm}.$$

From these equations, it follows that $k_0 \ \underline {= \ 2}$ and $k_1 \ \underline {= \ –1}$.

(2) The values $g_0 = 1$ and $g_1 = 0$ have already been used as a basis for the optimization and are therefore undisputed.

At time $t = 2T$, the output results, where $k_{-1} = k_1 = -1$:

$$g_2 = g_y(t = 2 T) = g_x(t = T) \cdot k_{-1}\hspace{0.15cm}\underline { = -0.5 = g_{-2}} \hspace{0.05cm}.$$

Since all input values are zero at times $2T$, $3T$ and $4T$ ⇒ $g_3 = g_y(t = 3T) \underline {= \ 0}$.
This gives the output pulse $g_y(t)$ as shown in the sketch.

(3) For a second order filter, the system of equations is:

$$t = 2T\hspace{-0.1cm}:\hspace{0.2cm}g_2 = k_1 \cdot 0.5 + k_2 \cdot 1.0 = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} k_2 = - 0.5 \cdot k_1\hspace{0.05cm},$$

Output pulse for $N = 2$

$$t = T\hspace{-0.1cm}:\hspace{0.2cm}g_1= k_0 \cdot 0.5 +k_1 \cdot 1.0 + k_2 \cdot 0.5 = 0\hspace{0.05cm},$$

$$\hspace{1.6cm}\Rightarrow \hspace{0.3cm} k_1 = - {2}/{3} \cdot k_0\hspace{0.05cm},$$

$$t = 0\hspace{-0.1cm}:\hspace{0.2cm}g_0 = k_0 \cdot 1.0 + k_1 \cdot 0.5 + k_1 \cdot 0.5 = 1\hspace{0.05cm},$$

$$\hspace{1.6cm}\Rightarrow \hspace{0.3cm} k_0 = 3 \hspace{0.05cm}.$$

Thus, the optimal coefficients are

$$k_0 \ \underline {= \ 3},k_1 \ \underline {= \ –2}, k_2 \ \underline {= \ 1}.$$

(4) Proceeding in the same way as in subtask (2), we obtain $g_4 \ \underline {= \ 0}$ as well as

$$g_3 = g_y(t = 3 T) = g_x(t = T) \cdot k_{-2} = 0.5 \cdot 1 \hspace{0.15cm}\underline {= 0.5} \hspace{0.05cm}.$$

However, the two graphs also show that for the triangular shape here, the optimal Nyquist equalization does not improve anything. The eye is "just closed" in all cases:

$$N = 0\hspace{-0.1cm}:\hspace{0.2cm} \ddot{o}/2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} g_0 - 2 \cdot g_1 = 1- 2 \cdot 0.5 = 0 \hspace{0.05cm}, $$

$$N = 1\hspace{-0.1cm}:\hspace{0.2cm} \ddot{o}/2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} g_0 - 2 \cdot |g_2 | = 1- 2 \cdot 0.5 = 0 \hspace{0.05cm}, $$

$$N = 2\hspace{-0.1cm}:\hspace{0.2cm} \ddot{o}/2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} g_0 - 2 \cdot g_3 = 1- 2 \cdot 0.5 = 0 \hspace{0.05cm}.$$