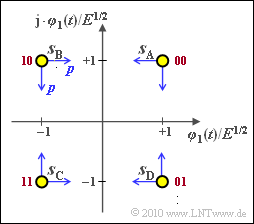
We now consider a quadrature amplitude modulation with $M = 4$ symbols and the (normalized) signal space points
- $$\boldsymbol{ s}_{\rm A} = (+1, +1)\hspace{0.05cm},\hspace{0.2cm}\boldsymbol{ s}_{\rm B} = (-1, +1)\hspace{0.05cm},\hspace{0.2cm} \boldsymbol{ s}_{\rm C} = (-1, -1)\hspace{0.05cm},\hspace{0.2cm}\boldsymbol{ s}_{\rm D} = (+1, -1) \hspace{0.05cm}.$$
The symbols are equally probable. Thus, averaging can be omitted to calculate the average symbol error probability.
For example:
- $$p_{\rm S} = {\rm Pr}({\cal{E}}) = {\rm Pr}( \boldsymbol{ s}_{\rm B} \cup \boldsymbol{ s}_{\rm C} \cup \boldsymbol{ s}_{\rm D} \hspace{0.15cm}{\rm decided} \hspace{0.05cm}|\hspace{0.05cm} \boldsymbol{ s}_{\rm A}\hspace{0.15cm} {\rm transmitted}) \hspace{0.05cm}.$$
The assignment of the symbols to "bit-duples" can also be taken from the graphic (red labels). Gray coding is assumed here.
Notes:
- The exercise belongs to the chapter "Carrier Frequency Systems with Coherent Demodulation".
- Reference is made in particular to the section "Quadrature amplitude modulation" $\rm (QAM)$.
- For subtask (4), the (discrete-time) AWGN channel with variance $\sigma_n^2 = N_0/2$ is assumed.
- For the probability that a symbol is falsified horizontally or vertically by the noise signal $n$, with the complementary Gaussian error function $\rm Q(x)$ holds:
- $$p = {\rm Pr}( n < -x_0) = {\rm Pr}( n > + x_0) = {\rm Q}(x_0 / \sigma_n) \hspace{0.05cm}.$$
Questions
Solution
- $$p_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}({\cal{E}}) = {\rm Pr}( {\cal{E}} \hspace{0.05cm}|\hspace{0.05cm} \boldsymbol{ s}_{\rm A}\hspace{0.15cm} {\rm transmitted})= {\rm Pr}( \boldsymbol{ s}_{\rm B} \cup \boldsymbol{ s}_{\rm C} \cup \boldsymbol{ s}_{\rm D} \hspace{0.15cm}{\rm decided} \hspace{0.05cm}|\hspace{0.05cm} \boldsymbol{ s}_{\rm A}\hspace{0.15cm} {\rm transmitted}) \hspace{0.05cm}.$$
- In contrast, for the (improved) "Union Bound" in the present example:
- $$p_{\rm UB} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}( \boldsymbol{ s}_{\rm B} \cup \boldsymbol{ s}_{\rm C} \hspace{0.15cm}{\rm decided} \hspace{0.05cm}|\hspace{0.05cm} \boldsymbol{ s}_{\rm A}\hspace{0.15cm} {\rm transmitted}) +{\rm Pr}( \boldsymbol{ s}_{\rm C} \cup \boldsymbol{ s}_{\rm D} \hspace{0.15cm}{\rm decided} \hspace{0.05cm}|\hspace{0.05cm} \boldsymbol{ s}_{\rm A}\hspace{0.15cm} {\rm transmitted}) = 2p = \underline{0.2} \hspace{0.05cm}.$$
(2) The two probabilities that make up the "Union Bound" additive can be interpreted geometrically as follows:
- ${\rm Pr}(\boldsymbol{s}_{\rm B} \cup \boldsymbol{s}_{\rm C} | \boldsymbol{s}_{\rm A})$ is the probability that the receiving point is located in the left half-plane
⇒ the AWGN noise component $n_1$ is negative and greater in magnitude than $\sqrt {E}$.
- ${\rm Pr}(\boldsymbol{s}_{\rm C} \cup \boldsymbol{s}_{\rm D} | \boldsymbol{s}_{\rm A})$ is the probability that the receiving point lies in the lower half-plane
⇒ the AWGN noise component $n_2$ is negative and greater in magnitude than $\sqrt {E}$.
Thus, the "Union Bound" considers the third quadrant twice. It is relatively easy to compensate for this error here:
- $$p_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} p_{\rm UB} - {\rm Pr}( \boldsymbol{ s}_{\rm C} \hspace{0.15cm}{\rm decided} \hspace{0.05cm}|\hspace{0.05cm} \boldsymbol{ s}_{\rm A}\hspace{0.15cm} {\rm transmitted}) = 2 p - {\rm Pr}\left [ ( n_1 < -\sqrt{E})\cap ( n_2 < -\sqrt{E})\right ] = 2p - p^2 = \underline{0.19} \hspace{0.05cm}.$$
Here it is considered that the noise components $n_1$ and $n_2$ are independent of each other.
(3) As proved in subtask (2), the following are valid for the individual falsification probabilities:
- Quadrant 2: ${\rm Pr}(\boldsymbol{s}_{\rm B} \ {\rm received} \ | \ \boldsymbol{s}_{\rm A} \ {\rm transmitted}) = 0.09$,
- Quadrant 3: ${\rm Pr}(\boldsymbol{s}_{\rm C} \ {\rm received} \ | \ \boldsymbol{s}_{\rm A} \ {\rm transmitted}) = 0.01$,
- Quadrant 4: ${\rm Pr}(\boldsymbol{s}_{\rm D} \ {\rm received} \ | \ \boldsymbol{s}_{\rm A} \ {\rm transmitted}) = 0.09$.
Thus, for the average bit error probability we obtain:
- $$p_{\rm B} = { 1}/{ 2} \cdot \big [ 1 \cdot 0.09 + 2 \cdot 0.01 + 1 \cdot 0.09\big ]= \underline{0.1} = p \hspace{0.05cm}.$$
- It is taken into account that "quadrant 2" and "quadrant 4" each lead to only one bit error, while "quadrant 3" leads to two.
- The factor $1/2$ considers again that in each case one symbol contains two binary characters (bits).
(4) According to the solution to subtask (2), the bit error probability is equal to the probability that the two noise components exceed certain limits:
- $$p_{\rm B} = {\rm Pr}( n_1 < -\sqrt{E}) = {\rm Pr}( n_2 < -\sqrt{E}) \hspace{0.05cm}.$$
- For the AWGN channel, this probability with variance $\sigma_n^2 = N_0/2$ is:
- $$p_{\rm B} = {\rm Q} \left ( { { \sqrt{E}}/{ \sigma_n} }\right ) = {\rm Q} \left ( \sqrt{ { {2E}}/{ N_0} }\right ) \hspace{0.05cm}.$$
- The average energy per symbol can be most easily determined by averaging over the squared distances of the signal space points from the origin.
This yields $E_{\rm S} = 2E$.
- The average energy per bit is half: $E_{\rm B} = E_{\rm S}/2 = E$. From this follows:
- $$p_{\rm B} = {\rm Q} \left ( \sqrt{ { {2E_{\rm B}}}/{ N_0} }\right ) \hspace{0.05cm}.$$
- The second solution is therefore correct.
- The same result is also obtained if the "4–QAM" is considered as two orthogonal (i.e.: not interfering with each other) BPSK systems over the same channel as in the chapter "Structure of the Optimal Receiver" of the book "Modulation methods".