Exercise 4.2: AM/PM Oscillations

• Return to book

Two possible AM/PM oscillations

We consider the signal set   $\{s_i(t)\}$   with the indexing variable  $i = 1, \ \text{...} \, M$.  All signals  $s_i(t)$  can be represented in the same way:

$$s_i(t) = \left\{ \begin{array}{c} A_i \cdot \cos(2\pi f_{\rm T}t + \phi_i) \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} 0 \le t < T \hspace{0.05cm}, \\ {\rm otherwise}\hspace{0.05cm}. \\ \end{array}$$

The signal duration  $T$  is an integer multiple of  $1/f_{\rm T}$,  where  $f_{\rm T}$  is the signal frequency  ("carrier frequency").

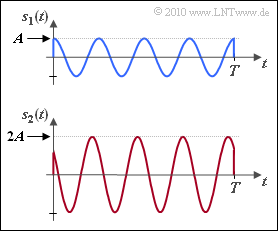
• For the sketch,  the duration of the energy-limited signals is  $T = 4/f_{\rm T}$,  i.e. exactly four oscillations are recognized within  $T$  in each case.

• The individual signals  $s_i(t)$  differ in amplitude  $(A_i)$  and/or phase  $(\phi_i)$.

For the two signals  (shown in the graph)  holds:

$$s_1(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} A \cdot \cos(2\pi f_{\rm T}t ) \hspace{0.05cm},$$

$$s_2(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2A \cdot \cos(2\pi f_{\rm T}t + \pi/4) \hspace{0.05cm}.$$

If we first restrict ourselves to these two signals  $s_1(t)$  and  $s_2(t)$,  they can be completely described by the basis functions  $\varphi_1(t)$  and  $\varphi_2(t)$.  These are orthonormal to each other,  that is,  taking into account the time constraint on  $T$  holds:

$$\int_{0}^{T}\varphi_1^2(t) \, {\rm d} t = \int_{0}^{T}\varphi_2^2(t) \, {\rm d} t = 1 \hspace{0.05cm},$$

$$\int_{0}^{T}\varphi_1(t) \cdot \varphi_2(t)\, {\rm d} t = 0 \hspace{0.05cm}.$$

With these basis functions,  the two signals can be represented as follows:

$$s_1(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} s_{11} \cdot \varphi_1(t) \hspace{0.05cm},$$

$$s_2(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} s_{21} \cdot \varphi_1(t) + s_{22} \cdot \varphi_2(t) \hspace{0.05cm}.$$

In subtask  (7)  we want to check whether all signals  $s_i(t)$  according to the above definition   $($with arbitrary amplitude  $A_i$  and arbitrary phase  $\phi_i)$   can be described by the following equation:

$$s_i(t)= s_{i1} \cdot \varphi_1(t) + s_{i2} \cdot \varphi_2(t) \hspace{0.05cm}.$$

The basis functions  $\varphi_1(t)$  and  $\varphi_2(t)$  are to be found here by the   "Gram–Schmidt process",   which was described in detail in the theory section.  The required equations are summarized here again:

$$\varphi_1(t) = \frac{s_1(t)}{||s_1(t)||}\hspace{0.4cm}{\rm with}\hspace{0.4cm} s_{11} = ||s_1(t)|| = \sqrt{\int_{0}^{T}s_1^2(t) \, {\rm d} t} \hspace{0.05cm},\hspace{0.4cm} s_{21} = \hspace{0.1cm} < \hspace{-0.1cm} s_2(t), \hspace{0.1cm}\varphi_1(t) \hspace{-0.1cm} > \hspace{0.1cm} = \int_{0}^{T}s_2(t) \cdot \varphi_1(t)\, {\rm d} t \hspace{0.05cm},$$

$$\theta_2(t) = s_2(t) - s_{21} \cdot \varphi_1(t)\hspace{0.05cm}, \hspace{0.2cm} \varphi_2(t) = \frac{\theta_2(t)}{||\theta_2(t)||}\hspace{0.05cm}.$$

Notes:

• The exercise belongs to the chapter  "Signals, Basis Functions and Vector Spaces".

• For abbreviation,  use the energy  $E = 1/2 \cdot A^2 \cdot T$.

• Furthermore,  the following trigonometric relation is given:  

$$\cos(\alpha \pm \beta) = \cos(\alpha )\cdot \cos(\beta) \mp \sin(\alpha )\cdot \sin(\beta)\hspace{0.05cm}.$$

Questions

1

What is the energy and the  "2–norm"  of the signal  $s_1(t)$,  expressed by  $E$?

$E_1\ = \ $ $\ \cdot E$

$||s_1(t)|| \ = \ $ $\ \cdot \sqrt{E}$

2

What is the Gram–Schmidt basis function  $\varphi_1(t)$? 

	$\varphi_1(t) = \sqrt{E} \cdot {\rm cos}(2\pi f_{\rm T}t)$,
	$\varphi_1(t) = \cos(2\pi f_{\rm T}t)$,
	$\varphi_1(t) = \sqrt{2/T} \cdot {\rm cos}(2\pi f_{\rm T}t)$.

3

What is the relationship between  $s_1(t)$  and  $\varphi_1(t)$?

	$s_1(t) = \sqrt{E} \cdot \varphi_1(t)$,
	$s_1(t) = A \cdot \varphi_1(t)$,
	$s_1(t) = \sqrt{2/T} \cdot \varphi_1(t)$.

4

What is the  "inner product"  $s_{\rm 21} = 〈 s_2(t) \cdot \varphi_1(t)〉$?

$s_{\rm 21} \ = \ $ $\ \cdot \sqrt{E}$

5

What is the auxiliary function  $\theta_2(t)$?

	$\theta_2(t) = +\sqrt{2} \cdot A \cdot {\rm sin}(2\pi f_{\rm T}t)$,
	$\theta_2(t) =-\sqrt{2} \cdot A \cdot {\rm sin}(2\pi f_{\rm T}t)$,
	$\theta_2(t) = \sqrt{2/T} \cdot {\rm sin}(2\pi f_{\rm T}t)$.

6

Give the coefficients of   $s_2(t) = s_{\rm 21} \cdot \varphi_1(t) + s_{\rm 22} \cdot \varphi_2(t)$. 

$s_{\rm 21}\ = \ $ $\ \cdot \sqrt{E}$

$s_{\rm 22}\ = \ $ $\ \cdot \sqrt{E}$

7

Which of the statements are generally true for the basis functions of the signal set  $\{s_i(t)\}$  with  $i = 1, \ \text{ ...} \ , M$,  if  $M \gg 2$?

	The number of basis functions is always  $N = M$.
	The number of basis functions is always  $N = 2$.
	Possible basis functions are cosine and (minus) sine.

Solution

Solution

(1)  The energy can be calculated using the following equation:

$$E_{1} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \int_{0}^{T}A^2 \cdot \cos^2(2\pi f_{\rm T}t )\, {\rm d} t = \frac{A^2 \cdot T}{2}\hspace{0.05cm}+\hspace{0.05cm} \frac{A^2 }{2}\int_{0}^{T} \cos(4\pi f_{\rm T}t )\, {\rm d} t = \frac{A^2 \cdot T}{2} \hspace{0.05cm}\underline{= 1 \cdot E} \hspace{0.05cm}.$$

• Here it is considered that  $T$  is an even multiple of  $1/f_{\rm T}$,  so the second integral vanishes.

• Further:

$$||s_1(t)|| = \sqrt{E_1} = \sqrt{E} = \hspace{0.1cm}\hspace{0.15cm}\underline{1 \cdot\sqrt{E}} \hspace{0.05cm}.$$

(2)  Solution 3  is correct:  The basis function  $\varphi_1(t)$  is equal in form to  $s_1(t)$,  where holds:

$$\varphi_1(t) = \frac{s_1(t)}{||s_1(t)||}= \frac{A \cdot \cos(2\pi f_{\rm T}t )}{\sqrt{E}}= \frac{A \cdot \cos(2\pi f_{\rm T}t )}{\sqrt{1/2 \cdot A^2 \cdot T}} = \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t ) \hspace{0.05cm}.$$

(3)  Solution 1  is correct  since according to the equation given in  (2):

$$s_1(t) = ||s_1(t)|| \cdot \varphi_1(t) = \sqrt{E} \cdot \varphi_1(t) \hspace{0.05cm}.$$

(4)  Using the signal  $s_2(t)$  according to the given information,  the basis function  $\varphi_1(t)$  according to subtask  (2)  and the given trigonometric relation we get:

$$s_{21} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \hspace{0.1cm} < \hspace{-0.1cm} s_2(t), \hspace{0.1cm}\varphi_1(t) \hspace{-0.1cm} > \hspace{0.1cm} = \int_{0}^{T}2A \cdot \cos(2\pi f_{\rm T}t + {\pi}/{4}) \cdot \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t )\, {\rm d} t =$$

$$\Rightarrow \hspace{0.3cm}s_{21} = \sqrt{\frac{8A^2}{T}}\cdot \int_{0}^{T}\cos({\pi}/{4}) \cdot \cos^2(2\pi f_{\rm T}t )\, {\rm d} t \hspace{0.1cm}- \sqrt{\frac{8A^2}{T}}\cdot \int_{0}^{T}\sin({\pi}/{4}) \cdot \sin(2\pi f_{\rm T}t )\cdot \cos(2\pi f_{\rm T}t )\, {\rm d} t \hspace{0.05cm}.$$

• The second component yields the value  $0$  (orthogonality).  The first component yields:

$$s_{21} = \sqrt{\frac{8A^2}{T}}\cdot \frac{1}{\sqrt{2}}\cdot \frac{T}{2} = \sqrt{A^2 \cdot T} = \sqrt{2E} \hspace{0.1cm}\hspace{0.15cm}\underline { = 1.414 \cdot \sqrt{E}} \hspace{0.05cm}.$$

(5)  According to the Gram–Schmidt process,  we obtain

$$\theta_2(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} s_2(t) - s_{21} \cdot \varphi_1(t)\hspace{0.05cm} = 2A \cdot \cos(2\pi f_{\rm T}t + {\pi}/{4}) - \sqrt{A^2 \cdot T} \cdot \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t )$$

$$\Rightarrow \hspace{0.3cm}\theta_2(t) = 2A \cdot \cos({\pi}/{4})\cdot \cos(2\pi f_{\rm T}t )\hspace{0.1cm} - \hspace{0.1cm} 2A \cdot \sin({\pi}/{4})\cdot \sin(2\pi f_{\rm T}t )\hspace{0.1cm} - \sqrt{2} \cdot A \cdot \cos(2\pi f_{\rm T}t ) \hspace{0.05cm}.$$

• With  $\cos {(\pi/4)} = \sin (\pi/4) =\sqrt{0.5}$  it follows:

$$\theta_2(t) = - \sqrt{2} \cdot A \cdot \sin(2\pi f_{\rm T}t ) \hspace{0.05cm}.$$

• Therefore,  solution 2 is correct.

(6)  Analogous to subtask  (2),  the orthonormal basis function  $\varphi_2(t)$  is given by

$$\varphi_2(t) = \frac{\theta_2(t)}{||\theta_2(t)||} = - \sqrt{{2}/{T}} \cdot \sin(2\pi f_{\rm T}t ) \hspace{0.05cm}.$$

• Thus,  the signal  $s_2(t)$  can be represented by  $s_{21}$  according to subtask  (4)  as follows:

$$s_2(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} s_{21} \cdot \varphi_1(t) + s_{22} \cdot \varphi_2(t) \hspace{0.05cm}, \hspace{0.2cm}s_{21} = \underline{ = 1.414 \cdot \sqrt {E}}\hspace{0.05cm},$$

$$s_{22}\hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{\theta_2(t)}{\varphi_2(t)} = \frac{-\sqrt{2} \cdot A \cdot \sin(2\pi f_{\rm T}t )} {-\sqrt{2/T}\cdot \sin(2\pi f_{\rm T}t )} = \sqrt{2} \cdot \sqrt{1/2 \cdot A^2 \cdot T}\hspace{0.05cm} \underline{ = 1.414 \cdot \sqrt {E}}\hspace{0.05cm}.$$

(7)  We consider very many energy-limited signals  $(M \gg 2)$  of the following form:

$$s_i(t)= \left\{ \begin{array}{c} A_i \cdot \cos(2\pi f_{\rm T}t + \phi_i) \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} 0 \le t < T \hspace{0.05cm}, \\ {\rm otherwise}\hspace{0.05cm}. \\ \end{array}$$

The indexing variable can take the values  $i = 1, 2, \ \text{...} \ , M$.  Then holds:

• All  $M$  signals can be completely described by only  $N = 2$  basis functions:

$$s_i(t)= s_{i1} \cdot \varphi_1(t) + s_{i2} \cdot \varphi_2(t) \hspace{0.05cm}.$$

• If one proceeds according to the Gram–Schmidt process,  one obtains for the two basis functions

$$\varphi_1(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t + \phi_1)\hspace{0.05cm},\hspace{0.5cm} \varphi_2(t) = \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t + \phi_1 \pm {\pi}/{2})\hspace{0.05cm}.$$

• The sign in the argument of the second cosine function  $(± \pi/2)$  is not unique.  Rather,  the sign of  $s_{i 2}$  also depends on whether the plus sign or the minus sign was used for  $\varphi_2(t)$.

• However,  possible basis functions that then lead to other coefficients are also:

$$\varphi_1(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t )\hspace{0.05cm},\hspace{0.5cm} \varphi_2(t) \pm \sqrt{{2}/{T}} \cdot \sin(2\pi f_{\rm T}t )\hspace{0.05cm}.$$

⇒   So the  solutions 2 and 3  are correct.