Exercise 4.2: Mismatched Line

• Return to book

Transmission line with wiring

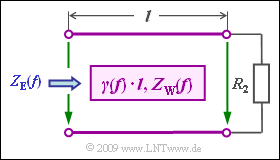
A transmission system occupies the range from  $f_{\rm U} = 10 \ \rm MHz$  to  $f_{\rm O} = 40 \ \rm MHz$.

The transmission line used has a constant wave impedance   $Z_{\rm W} = 100 \ \rm \Omega$  (real),  which does not quite correspond to reality,  since the wave impedance usually decreases slightly with frequency and often an imaginary part  (usually smaller)  must also be taken into account.

The line is supplied by a voltage source with internal resistance  $R_{\rm 1} = 100 \ \rm \Omega$  and is terminated by resistor  $R_{\rm 2}$.  The input impedance  (German:  "Eingangswiderstand"   ⇒   subscript  "E")  of the line is given by

$$Z_{\rm E}(f) = Z_{\rm W}\cdot \frac {R_2 + Z_{\rm W} \cdot {\rm tanh}(\gamma(f) \cdot l)} {Z_{\rm W}+ R_2 \cdot {\rm tanh}(\gamma(f) \cdot l)} \hspace{0.05cm},\hspace{0.3cm}{\rm tanh}(x) = \frac {{\rm e}^{x}-{\rm e}^{-x}}{{\rm e}^{x}+{\rm e}^{-x}}\hspace{0.05cm}, \hspace{0.3cm}x \in {\cal C} \hspace{0.05cm}.$$

The complex propagation function should – again very simplified – approximated by a real function:

$$\frac {\gamma(f)}{1\,{\rm Np/km}} = \frac {\alpha(f)}{1\,{\rm Np/km}} = \sqrt{f/f_{\rm O}} \hspace{0.05cm}, \hspace{0.3cm}f_{\rm O} = 40\,{\rm MHz}\hspace{0.05cm}.$$

Notes:

• The exercise belongs to the chapter  Some Results from Line Transmission Theory.
• In particular,  it should be examined whether there are reflections.
• To avoid confusion: 

1. $f_{\rm U}$  stands for  "lowest frequency"   ⇒   German:   "unterste Frequenz"   ⇒   subscript "U",
2. $f_{\rm O}$  stands for  "highest frequency"  ⇒   German:   "oberste Frequenz"   ⇒   subscript "O".

Questions

1

Which statements are valid for the wave impedance  $Z_{\rm W}$  of a line in general?

	$Z_{\rm W}$  depends on the line length.
	$Z_{\rm W}$  can be frequency dependent.
	$Z_{\rm W}$  can take on complex values at certain frequencies.

2

Which statements are valid for the wiring with  $R_1 = R_2 = Z_{\rm W}$?

	The input impedance  $Z_{\rm E}(f)$  is equal to the wave impedance.
	The input impedance  $Z_{\rm E}(f)$  is frequency independent.
	The input impedance  $Z_{\rm E}(f)$  depends on the line length.
	$R_1 = R_2 =Z_{\rm W}$ indicates the best possible wiring.

3

At which line length  $l = l_\text{min}$  do  $Z_{\rm E}$  and  $Z_{\rm W}$  differ by less than  $1\%$ in the  short-circuit case   $(R_{\rm 2} = 0)$ ?

$f_{\rm U} = 10\ {\rm MHz}\hspace{-0.1cm}:\hspace{0.2cm} l_\text{min}\ = \ $ $\ \rm km$

$f_{\rm O} = 40\ {\rm MHz}\hspace{-0.1cm}:\hspace{0.2cm} l_\text{min}\ = \ $ $\ \rm km$

4

At what line length  $l = l_\text{min}$  do  $Z_{\rm E}$  differ from  $Z_{\rm W}$  in  idle   $(R_2 → ∞)$ by less than  $1\%$?

$f_{\rm U} = 10\ {\rm MHz}\hspace{-0.1cm}:\hspace{0.2cm} l_\text{min}\ = \ $ $\ \rm km$

$f_{\rm O} = 40\ {\rm MHz}\hspace{-0.1cm}:\hspace{0.2cm} l_\text{min}\ = \ $ $\ \rm km$

Solution

Solution

(1)  Solutions 2 and 3 are correct:

• The wave impedance  $Z_{\rm W}$  is defined as the quotient of voltage and current of the wave propagating along the line.
• The wave impedance   $Z_{\rm W}$  is independent of the location.
• Therefore,  $Z_{\rm W}$  is also independent of the line length  $l$  and is determined solely by the primary line parameters $R\hspace{0.05cm}'$, $L\hspace{0.05cm}'$, $G\hspace{0.08cm}'$ and $C\hspace{0.08cm}'$.
• The following equation given in the theory section

$$Z_{\rm W}(f) = \sqrt{\frac {R\hspace{0.05cm}' + {\rm j} \cdot \omega L\hspace{0.05cm}'}{G\hspace{0.08cm}' + {\rm j} \cdot \omega C\hspace{0.08cm}'}} \hspace{0.1cm}\bigg |_{\hspace{0.05cm} \omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}$$

makes it clear that the wave impedance does depend on the frequency and is generally also complex-valued.

It should be noted that wave impedance is not a resistor in the sense of a user:

• The wave impedance does not characterize the line as a lossy element.
• Even a lossless line has a wave impedance.
• Similarly, a wave impedance is always defined in the propagation of an electromagnetic wave.

(2)  With the terminating resistor  $Z_{\rm 2}(f) = Z_{\rm W}(f)$  the resistance value transformed to the beginning of the line is also equal to the characteristic impedance, independent of the line length:

$$Z_{\rm E}(f) = Z_{\rm W}(f)\cdot \frac {Z_{\rm 2}(f) + Z_{\rm W}(f) \cdot {\rm tanh}(\gamma(f) \cdot l)} {Z_{\rm W}(f)+ Z_{\rm 2}(f) \cdot {\rm tanh}(\gamma(f) \cdot l)}= Z_{\rm W}(f)\cdot \frac {Z_{\rm W}(f) + Z_{\rm W}(f) \cdot {\rm tanh}(\gamma(f) \cdot l)} {Z_{\rm W}(f)+ Z_{\rm W}(f) \cdot {\rm tanh}(\gamma(f) \cdot l)}= Z_{\rm W}(f) \hspace{0.05cm}.$$

Solutions 1, 2 and 4 are correct:

• Since  $Z_{\rm W}(f) = Z_{\rm W}$  was assumed to be frequency-independent in the exercise, the input impedance  $Z_{\rm E}(f) = Z_{\rm E}$  is also frequency-independent.
• In contrast, with frequency-dependent wave impedance with real termination, reflections cannot be avoided for all frequencies.
• The wiring  $R_1 = R_2 =Z_{\rm W}$   ⇒   $R_1 =Z_{\rm E}$  is to be aimed at, since then the maximum power is delivered by the source.

(3)  With the terminating resistor  $R_{\rm 2} = 0$   ⇒   short circuit follows from the given equation with real  $x = \gamma (f) \cdot l$:

$$\frac{Z_{\rm E}(f)}{Z_{\rm W}} = {\rm tanh}(x) = \frac {{\rm e}^{x}-{\rm e}^{-x}}{{\rm e}^{x}+{\rm e}^{-x}}= \frac {{\rm e}^{2x}-1}{{\rm e}^{2x}+1}.$$

In particular:

$${Z_{\rm E}(f)}/{Z_{\rm W}} = 0.99 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\rm e}^{2x} = 199\hspace{0.3cm}\Rightarrow \hspace{0.3cm} x ={1}/{2}\cdot {\rm ln}\hspace{0.1cm}(199) \approx 2.65\,{\rm Np}\hspace{0.05cm}.$$

$$f_{\rm U} = 10\,\text {MHz:}\hspace{0.2cm}\alpha(f_{\rm U})= 0.5\,{\rm Np/km}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}l_{\rm min}= \frac{2.65\,{\rm Np}}{0.5\,{\rm Np/km}}\hspace{0.15cm}\underline{= 5.3\,{\rm km}} \hspace{0.05cm},$$

$$f_{\rm O} = 40\,\text {MHz:}\hspace{0.2cm}\alpha(f_{\rm U})= 1.0\,{\rm Np/km}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}l_{\rm min}= \frac{2.65\,{\rm Np}}{1.0\,{\rm Np/km}}\hspace{0.15cm}\underline{= 2.65\,{\rm km}} \hspace{0.05cm}.$$

That means:

• At the frequency  $f_{\rm O} = 40\ {\rm MHz}$ , the line length  $l= 2.65 \ \rm km$ is already sufficient to largely suppress reflections.
• At a lower frequency  $f_{\rm U} = 10\ {\rm MHz}$ , a longer cable length is required due to the lower attenuation function.
• Of course, these statements only refer to the avoidance of reflections.
• Overall, of course, the lower signal frequency is more favorable than the higher one.

(4)  Similarly, one obtains for  $R_2 → ∞$   ⇒   idle:

$$\frac{Z_{\rm E}(f)}{Z_{\rm W}} = \frac{1}{{\rm tanh}(x)} = \frac {{\rm e}^{2x}+1}{{\rm e}^{2x}-1}\hspace{0.05cm}.$$

In contrast to the short-circuit case, this now results in the quotient  $Z_{\rm E}/Z_{\rm W} > 1$:

$${Z_{\rm E}(f)}/{Z_{\rm W}} = 1.01 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\rm e}^{2x} = 201\hspace{0.3cm}\Rightarrow \hspace{0.3cm} x ={1}/{2}\cdot{\rm ln}\hspace{0.1cm}(201) \approx 2.65\,{\rm Np}\hspace{0.05cm}.$$

Approximately, the same result is obtained here as in subtask  (3):

• At the frequency  $f_{\rm O} = 40\ {\rm MHz}$ , the line length  $l= 2.65 \ \rm km$ is already sufficient to largely suppress reflections.
• At a lower frequency  $f_{\rm U} = 10\ {\rm MHz}$ , a longer cable length is required due to the lower attenuation function.