Exercise 4.5Z: Impulse Response once again
As in Exercise 4.5 , we consider a binary transmission system with bit rate $R$ ⇒ symbol duration $T= 1/R$.
A "standard coaxial cable" $\text{(2.6 mm}$ core diameter, $\text{9.5 mm}$ outer diameter$)$ of length $l = 1 \ \rm km$ with the following frequency response is used as transmission medium:
- $$H_{\rm K}(f) = {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \beta_1 \hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm}l} \cdot {\rm e}^{- \alpha_2 \hspace{0.01cm} \sqrt{f} \hspace{0.05cm}l} \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \beta_2 \hspace{0.05cm}\cdot \hspace{0.05cm} \sqrt{f} \hspace{0.05cm}\cdot \hspace{0.05cm}l} = H_1(f) \cdot H_2(f) \cdot H_3(f)$$
The partial frequency responses $H_1(f)$, $H_2(f)$ and $H_3(f)$ are used here only as abbreviations. The line parameters are:
- $$\beta_1 = 21.78\, \frac{\rm rad}{\rm km \cdot MHz}\hspace{0.05cm}, $$
- $$ \alpha_2 = 0.2722\, \frac{\rm Np}{\rm km \cdot \sqrt{MHz}}\hspace{0.05cm},$$
- $$ \beta_2 = 0.2722\, \frac{\rm rad}{\rm km \cdot \sqrt{MHz}} \hspace{0.05cm}.$$
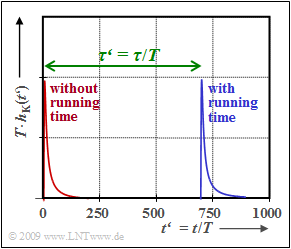
The graph shows the resulting impulse response $h_{\rm K}(t\hspace{0.05cm}')$, where $t\hspace{0.05cm}' = t/T$ represents the normalized time. Without considering the (normalized) phase running time $\tau\hspace{0.05cm}' = \tau/T$ , $h_{\rm K}(t\hspace{0.05cm}')$ can be written as follows:
- $$h_{\rm K}(t\hspace{0.05cm}') = \frac {1}{T} \cdot \frac {a_\rm \star/\pi}{ \sqrt{2 \hspace{0.05cm}t\hspace{0.05cm}'^3}}\cdot {\rm e}^{ -{a_\rm \star^2}/( {2\pi \hspace{0.05cm}t\hspace{0.05cm}')} } \hspace{0.05cm}, \hspace{0.2cm} \hspace{0.15cm} {\rm with}\hspace{0.15cm}{a}_{\rm \star}\hspace{0.15cm} {\rm in}\hspace{0.15cm} {\rm Neper}\hspace{0.05cm}.$$
- This equation gives the Fourier retransform of the product $H_2(f) \cdot H_3(f)$ .
- The characteristic cable attenuation ${a}_{\rm \star} = \alpha_2 \cdot \sqrt {R/2} \cdot l \hspace{0.05cm}$ is used here.
Notes:
- The exercise belongs to the chapter Properties of Coaxial Cables.
- You can use the (German language) interactive SWF applet "Zeitverhalten von Kupferkabeln" ⇒ "Time behavior of copper cables" to check your results.
- In Exercise 4.5 the maximum value of the normalized impulse response was calculated as follows:
- $${\rm Max}\, \big[T \cdot h_{\rm K}(t)\big ] = \frac {\sqrt{13.5 \pi} \cdot {\rm e}^{-1.5} }{{a}_{\rm \star}^2} \approx \frac {1.453 }{{a}_{\rm \star}^2} \hspace{0.05cm}, \hspace{0.2cm} \hspace{0.15cm} {\rm with}\hspace{0.15cm}{a}_{\rm \star}\hspace{0.15cm} {\rm in}\hspace{0.15cm} {\rm Neper}\hspace{0.05cm}.$$
Questions
Solution
- The spectral representation of a running time term is ${\rm e}^{-{\rm j} \hspace{0.05cm}\cdot\hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot\hspace{0.05cm} f \hspace{0.05cm}\cdot\hspace{0.05cm}\tau}$.
- A comparison with the information provided shows that $H_1(f)$ exactly satisfies this approach.
(2) According to the information provided, the following applies:
- $$2\pi \cdot f \cdot \tau = \beta_1 \cdot f \cdot l \Rightarrow \hspace{0.3cm}\tau= \frac {\beta_1 \cdot l}{2\pi} = \frac {21.78\, {\rm rad}/{({\rm km \cdot MHz})}\cdot 10\,{\rm km}}{2\pi} = 34.7\,{\rm µ s}$$
- $$\Rightarrow \hspace{0.3cm}\tau '= {\tau}/{T} = 694 \Rightarrow \hspace{0.3cm} T = \frac {34.7\,{\rm µ s}}{700} \approx 0.05\,{\rm µ s}\hspace{0.05cm}.$$
- The bit rate is equal to the reciprocal of the symbol duration:
- $$\underline{R = 20 \ \rm Mbit/s}.$$
(3) For the characteristic cable attenuation one obtains:
- $${a}_{\rm \star} = \alpha_2 \cdot \sqrt {R/2} \cdot l = 0.2722\, \frac{\rm Np}{\rm km \cdot \sqrt{MHz}} \cdot \sqrt {10\,{\rm MHz}} \cdot 10\,{\rm km} \hspace{0.15cm}\underline{\approx 8.6\,{\rm Np}}\hspace{0.05cm}.$$
- The corresponding dB value is ${a}_{\rm \star} = 75 \ \rm dB$.
(4) Using the given equation and the result of subtask (3) , we obtain:
- $${\rm Max}\, \big[T \cdot h_{\rm K}(t)\big] \approx \frac {1.453 }{{a}_{\rm \star}^2} = \frac {1.453 }{8.6^2} \hspace{0.15cm}\underline{ \approx 0.02}\hspace{0.05cm}.$$
(5) Only solution 1 is correct: $H_1(f)$ describes the frequency-independent running time which does not result in any distortion.
On the other hand, $H_2(f)$ or $H_3(f)$ should never be omitted for the calculation of the impulse response, otherwise serious errors would occur:
- The impulse response $h_2(t)$ as the Fourier retransform of $H_2(f)$ is an even function with the maximum at $t = 0$ and extends in both directions over hundreds of symbols.
- In contrast, the Fourier retransform of $H_3(f)$ is an odd function with a point of discontinuity at $t = 0$.
- For $t > 0$ , $h_3(t)$ drops similarly – but not exactly – to an exponential function. For negative times $t$ , $h_3(t) = - h_3(|t|)$ is valid.
- Only the convolution $h_2(t) \star h_3(t)$ yields the causal impulse response, but without the phase running time $\tau$, which is considered in this model by $H_1(f)$ .