Exercise 4.7Z: About the Water Filling Algorithm

• Return to book

Water-filling principle  $(K = 4)$

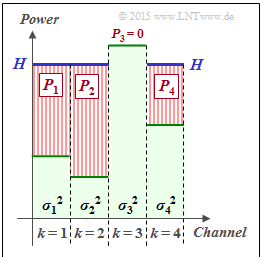
We consider  $K$  parallel Gaussian channels  $\rm (AWGN)$  with different interference powers  $\sigma_k^2$,  where  $1 \le k \le K$ .  The graph illustrates this constellation using  $K = 4$  as an example.

The transmission power in the individual channels is denoted by  $P_k$,  the sum of which must not exceed the specified value $P_X$ :

$$P_1 +\text{...}\hspace{0.05cm}+ P_K = \hspace{0.1cm} \sum_{k= 1}^K \hspace{0.1cm}{\rm E} \left [ X_k^2\right ] \le P_{X} \hspace{0.05cm}.$$

If the random variables  $X_1$, ... , $X_K$  are Gaussian, then for the (total) mutual information between the input  $X$  and the output  $Y$  can be written:

$$I(X_1,\text{...} \hspace{0.05cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1, \text{...}\hspace{0.05cm}, Y_K) = 1/2 \cdot \sum_{k= 1}^K \hspace{0.1cm} {\rm log}_2 \hspace{0.1cm} ( 1 + \frac{P_k}{\sigma_k^2})\hspace{0.05cm},\hspace{0.5cm} {\rm Result\hspace{0.15cm} in \hspace{0.15cm} \text{"bit"} } \hspace{0.05cm}.$$

The maximum for this is the  channel capacity of the total system,  where the maximization refers to the division of the total power  $P_X$  among the individual channels:

$$C_K(P_X) = \max_{P_k\hspace{0.05cm},\hspace{0.15cm}{\rm with} \hspace{0.15cm}P_1 + ... \hspace{0.05cm}+ P_K = P_X} \hspace{-0.5cm} I(X_1, \text{...} \hspace{0.05cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1, \text{...}\hspace{0.05cm}, Y_K) \hspace{0.05cm}.$$

This maximization can be done with the  "water–filling algorithm"  shown in the above graph for  $K = 4$.

In the present exercise, this algorithm is to be applied, assuming the following:

• Two parallel Gaussian channels   ⇒   $K = 2$,
• normalized noise powers   $\sigma_1^2 = 1$   and   $\sigma_2^2 = 4$,
• normalized transmission powers   $P_X = 10$   and   $P_X = 3$ respectively.

Hints:

• The exercise belongs to the chapter  AWGN channel capacity with continuous value input.
• Reference is made in particular to the page  Parallel Gaussian Channels.
• Since the results are to be given in  "bit",  the logarithm to base  $2$  is used in the equations:   $\log_2$.

Questions

1

Which power allocation strategies are useful?

	A very noisy channel  $k$  $($with large noise power  $\sigma_k^2)$  should be allocated a large effective power  $P_k$.
	A very noisy channel  $k$  $($with large noise power  $\sigma_k^2)$  should be assigned only a small useful power  $P_k$.
	For  $K$  equally good channels   ⇒   $\sigma_1^2 = \text{...} = \sigma_K^2 = \sigma_N^2$  the power  $P_k$  should be evenly distributed.

2

What is the mutual information obtained by distributing the transmission power  $P_X = 10$  equally to both channels   $(P_1= P_2 = 5)$?

$I(X_1, X_2; Y_1, Y_2) \ = \ $ $\ \rm bit$

3

Let  $P_X = P_1 + P_2 = 10$  be further valid.  Which optimal power distribution results according to the  "water–filling algorithm"?

$P_1 \ = \ $

$P_2 \ = \ $

4

What is the channel capacity for  $\underline{K = 2}$  and  $\underline{P_X = 10}$?

$C \ = \ $ $\ \rm bit$

5

What mutual information results if the transmit power  $P_X = 3$  is distributed equally to both channels   $(P_1= P_2 = 1.5)$?

$I(X_1, X_2; Y_1, Y_2) \ = \ $ $\ \rm bit$

6

What is the channel capacity for  $\underline{K = 2}$  and  $\underline{P_X = 3}$?

$C \ = \ $ $\ \rm bit$

Solution

Solution

(1)  Proposed solutions 2 and 3  are correct:

• According to the explanations in the theory section  "Water–Filling"   ⇒   Proposal 2  is to be applied when unequal conditions exist.
• However,  solution proposal 3  is also correct:   If the channels are equally good, there is nothing to prevent all  $K$  channels from being filled with the same power   ⇒    $P_1 = P_2 =$  ...  $= P_K = P_X/K$.

(2)  For the mutual information, with equal power distribution, the following applies:

$$I(X_1, X_2\hspace{0.05cm};\hspace{0.05cm}Y_1, Y_2) \ = \ {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{5}{1} \right ) +{1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{5}{4} \right )=1.292\,{\rm bit}+ 0.585\,{\rm bit} \hspace{0.15cm}\underline{= 1.877\,{\rm bit}} \hspace{0.05cm}.$$

Best possible distribution of transmit power  $P_X = 10$

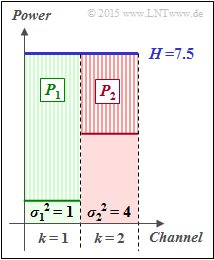
(3)  According to the adjacent sketch, the following must apply:

$$P_2 = P_1 - (\sigma_2^2 - \sigma_1^2) = P_1 -3\hspace{0.3cm}\text{wobei }\hspace{0.3cm}P_1 + P_2 = P_X = 10$$

$$\Rightarrow \hspace{0.3cm} P_1 + (P_1 -3) = 10\hspace{0.3cm}\Rightarrow \hspace{0.3cm} 2 \cdot P_1 = 13 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{P_1 = 6.5}\hspace{0.05cm}, \hspace{0.3cm}\underline{P_2 = 3.5}\hspace{0.05cm}.$$

For the  "water level height"  here holds: 

$$H= P_1 + \sigma_1^2= P_2 + \sigma_2^2 = 7.5 = 6.5+1 = 3.5+4.$$

(4)  The channel capacity indicates the maximum mutual information.   The maximum is already fixed by the best possible power sharing according to subtask (3). For  $P_X = 10$  holds:

$$C={1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{6.5}{1} \right ) +{1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{3.5}{4} \right )$$

$$\Rightarrow\hspace{0.3cm} C=1.453\,{\rm bit}+ 0.453\,{\rm bit} \hspace{0.15cm}\underline{= 1.906\,{\rm bit}} \hspace{0.05cm}.$$

(5)  For  $P_X = 3$,   with the same power splitting  $(P_1 = P_2 =1.5)$,  we obtain:

$$I(X_1, X_2\hspace{0.05cm};\hspace{0.05cm}Y_1, Y_2) ={1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{1.5}{1} \right ) +{1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{1.5}{4} \right ) \hspace{0.15cm}\underline{= 0.891\,{\rm bit}} \hspace{0.05cm}.$$

Best possible distribution of the transmit power  $P_X = 3$

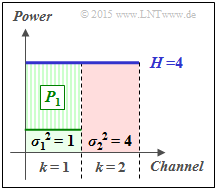
(6)  According to the water–filling algorithm, the total transmission power  $P_X = 3$  is now fully allocated to the first channel:

$${P_1 = 3}\hspace{0.05cm}, \hspace{0.3cm}{P_2 = 0}\hspace{0.05cm}.$$

• So here for the  "water level height": 

$$H= 4= P_1 + \sigma_1^2= P_2 + \sigma_2^2= 3+1=0+4.$$

• This gives for the channel capacity:

$$C ={1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{3}{1} \right ) +{1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{0}{4} \right )=1\,{\rm bit}+ 0\,{\rm bit} \hspace{0.15cm}\underline{= 1\,{\rm bit}} \hspace{0.05cm}.$$

Further notes:

• While for  $P_X = 10$  the difference between even and best power splitting was only  $0.03$  bit, for  $P_X = 3$  the difference is larger:  $0.109$  bit.
• For even larger  $P_X > 10$ , the difference between even and best power splitting becomes even smaller.

For example, for  $P_X = 100$  the difference is only   $0.001$  bit as the following calculation shows:

• For  $P_1 = P_2 = 50$  one obtains:

$$I = I(X_1, X_2\hspace{0.05cm};\hspace{0.05cm}Y_1, Y_2) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{50}{1} \right ) +{1}/{2}\cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{50}{4} \right )= 2.836\,{\rm bit}+ 1.877\,{\rm bit} \hspace{0.15cm}\underline{= 4.713\,{\rm bit}} \hspace{0.05cm}.$$

• In contrast, the best possible split gives   ⇒   $P_1 = 51.5, \ P_2 = 48.5$:

$$C = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{51.5}{1} \right ) +{1}/{2}\cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{48.5}{4} \right )= 2.857\,{\rm bit}+ 1.857\,{\rm bit} \hspace{0.15cm}\underline{= 4.714\,{\rm bit}} \hspace{0.05cm}.$$