Exercise 4.9: Higher-Level Modulation
From LNTwww
(Redirected from Aufgabe 4.9: Höherstufige Modulation)
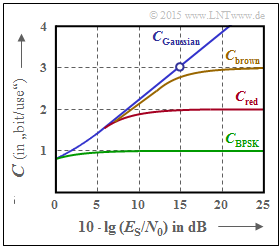
The graph shows AWGN channel capacity curves over the $10 \cdot \lg (E_{\rm S}/{N_0})$:
- $C_\text{Gaussian}$: Shannon's boundary curve,
- $C_\text{BPSK}$: valid for "Binary Phase Shift Keying".
The two other curves $C_\text{red}$ and $C_\text{brown}$ should be analyzed and assigned to possible modulation schemes in subtasks (3) and (4).
Hints:
- The task belongs to the chapter AWGN channel capacity with discrete value input.
- Reference is made in particular to the page Channel capacity $C$ as a function of $E_{\rm S}/{N_0}$.
- Since the results are to be given in "bit" ⇒ "log" ⇒ "log2" is used in the equations.
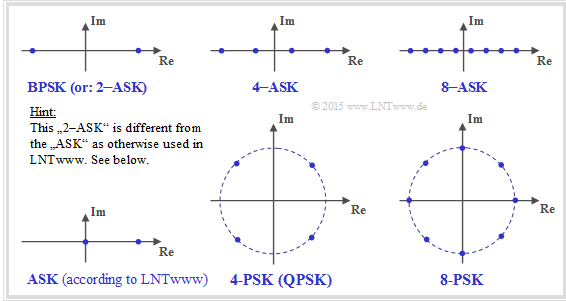
- The modulation methods mentioned in the questions are described in terms of their signal space constellation
(see lower graph).
Notes on nomenclature:
- In the literature, "BPSK" is sometimes also referred to as "2–ASK":
- $$x ∈ X = \{+1,\ -1\}.$$
- In contrast, in our learning tutorial we understand as "ASK" the unipolar case:
- $$x ∈ X = \{0,\ 1 \}.$$
- Therefore, according to our nomenclature:
- $$C_\text{ASK} < C_\text{BPSK}$$
But: This fact is irrelevant for the solution of the present problem.
Questions
Solution
(1) Proposition 2 is correct, as shown by the calculation for $10 \cdot \lg (E_{\rm S}/{N_0}) = 15 \ \rm dB$ ⇒ $E_{\rm S}/{N_0} = 31.62$:
- $$C_2(15\hspace{0.1cm}{\rm dB}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + 2 \cdot 31.62 ) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 64.25 ) \approx 3\,{\rm bit/use}\hspace{0.05cm}. $$
- The other two proposed solutions provide the following numerical values:
- $$C_3(15\hspace{0.1cm}{\rm dB}) \ = \ {\rm log}_2 \hspace{0.1cm} ( 1 + 31.62 ) \approx 5.03\,{\rm bit/use}\hspace{0.05cm},$$
- $$ C_1(15\hspace{0.1cm}{\rm dB}) \ = \ C_3/2 \approx 2.51\,{\rm bit/use}\hspace{0.05cm}.$$
- The proposed solution 3 corresponds to the case of "two independent Gaussian channels" with half transmission power per channel.
(2) Proposed solutions 1, 2 and 4 are correct:
- If one would replace $E_{\rm S}$ by $E_{\rm B}$, then the statement 3 would be also correct.
- For $E_{\rm B}/{N_0} < \ln (2)$ ⇒ $C_{\rm Gaussian} ≡ 0$ is valid, and therefore also $C_{\rm BPSK} ≡ 0$.
(3) Statements 2, 3 and 5 are correct:
- The red curve $(C_{\rm red})$ is always above $C_{\rm BPSK}$, but below $C_{\rm brown}$ and Shannon's boundary curve $(C_{\rm Gaussian})$.
- The statements also hold if (for certain $E_{\rm S}/{N_0}$ values) curves are indistinguishable within the drawing precision.
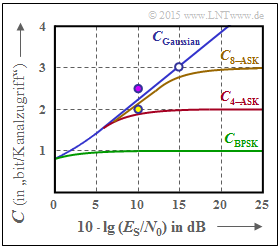
- From the limit $C_{\rm red}= 2 \ \rm bit/use$ for $E_{\rm S}/{N_0} → ∞$, the symbol set size $M_X = |X| = 4$.
- Thus, the red curve describes "4–ASK". $M_X = |X| = 2$ would apply to the "BPSK".
- The "4–QAM" leads exactly to the same final value "2 bit/use". For small $E_{\rm S}/{N_0}$ values, however, the channel capacity $C_{\rm 4–QAM}$ is above the red curve, since $C_{\rm red}$ is bounded by the Gaussian boundary curve $(C_2)$, but $C_{\rm 4–QAM}$ is bounded by $C_3$. The designations $C_2$ and $C_3$ here refer to subtask '(1)
(4) Proposed solutions 1, 2 and 5 are correct:
- From the brown curve, one can see the correctness of the first two statements.
- The "8–PSK" with I– and Q–components – i.e. with $K = 2$ dimensions – lies slightly above the brown curve for small $E_{\rm S}/{N_0}$ values ⇒ the answer 3 is incorrect.
In the graph, the two "8–ASK"nbsp; systems are also drawn as dots according to propositions 4 and 5.
- The purple dot is above the $C_{\rm 8–ASK}$ curve ⇒ $R = 2.5$ and $10 \cdot \lg (E_{\rm S}/{N_0}) = 10 \ \rm dB$ are not enough to decode the "8–ASK" without errors ⇒ $R > C_{\rm 8–ASK}$ ⇒ channel coding theorem is not satisfied ⇒ answer 4 is wrong.
- However, if we reduce the code rate to $R = 2 < C_{\rm 8–ASK}$ for the same $10 \cdot \lg (E_{\rm S}/{N_0}) = 10 \ \rm dB$ according to the yellow dot, the channel coding theorem is satisfied ⇒ answer 5 is correct.