Exercise 5.7: Rectangular Matched Filter

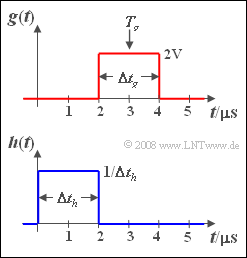
Pulse $g(t)$ and Matched Filter impulse response $h(t)$

At the input of a lowpass filter with a rectangular impulse response $h(t)$ the reception signal $r(t)$ is present, which is additively composed of a pulse-shaped signal component $g(t)$ and a noise component $n(t)$. It holds:

The pulse $g(t)$ is rectangular.
The pulse duration is $\Delta t_g = 2 \hspace{0.08cm}\rm µ s$.
The pulse amplitude is $g_0 = 2 \hspace{0.08cm}\rm V$.
The center of the pulse is at $T_g = 3 \hspace{0.08cm}\rm µ s$.
The noise $n(t)$ is white and Gaussian distributed.
The power density is $N_0 = 4 \cdot 10^{-6} \hspace{0.08cm}\rm V^2\hspace{-0.1cm}/Hz$ with respect to the $1 \hspace{0.08cm}\rm \Omega$ resistor.

The rectangular impulse response of the filter starts at $t = 0$.

The impulse response duration $\Delta t_h$ is freely selectable.
The height $1/\Delta t_h$ of the impulse response is adjusted in each case so that $H(f = 0) = 1$.

Notes:

The exercise belongs to the chapter Matched Filter.
For the questions (1) to (6): $\Delta t_h =\Delta t_g = 2 \hspace{0.05cm}\rm µ s$ always applies.

Questions

Solution

(1) Solutions 1 and 3 are correct:

For the same pulse duration $(\Delta t_h =\Delta t_g)$, there is a matched filter, even if $g(t)$ and $h(t)$ differ in amplitude and temporal position.
Thus, there is no other filter with better signal–to–noise power ratio.
The filter with rectangular impulse response can also be interpreted as an integrator over the time duration $\Delta t_h$.

(2) The impulse response of the matched filter is: $h_{\rm MF} (t) = K_{\rm MF} \cdot g(T_{\rm D} - t).$

The input impulse $g(t)$ is non-zero in the range from $2 \hspace{0.05cm}\rm µ s$ to $4 \hspace{0.08cm}\rm µ s$, and in the range from $-4 \hspace{0.08cm}\rm µ s$ to $-2 \hspace{0.08cm}\rm µ s$, when mirrored.
After shifting by $4 \hspace{0.08cm}\rm µ s$, it is achieved that $g(T_{\rm D} - t)$ is, like the impulse response $h(t)$, between $0$ and $2 \hspace{0.08cm}\rm µ s$.
From this follows: $T_\text{D, opt}\hspace{0.15cm}\underline{ =4 \hspace{0.08cm}\rm µ s}$.

(3) With $\Delta t_h =\Delta t_g = 2 \cdot 10^{-6}\hspace{0.05cm}\rm µ s$ and $g_0 = 2 \hspace{0.08cm}\rm V$, we obtain $K_{\rm MF} = 1/(\Delta t_g \cdot g_0)\hspace{0.15cm}\underline{ =0.25 \cdot 10^{6}\hspace{0.08cm}\rm (1/Vs)}$.

(4) The energy of the pulse $g(t)$ is $E_g = g_0^2 \cdot \Delta t_g = 8 \cdot 10^{-6}\hspace{0.05cm}\rm V^2s$.

From this it follows for the maximum S/N ratio:

$$\rho _d (T_{{\rm{D, \hspace{0.08cm}opt}}} ) = \frac{2 \cdot E_g }{N_0 } = \frac{{2 \cdot 8 \cdot 10^{ - 6} \;{\rm{V}}^2 {\rm{s}}}}{{4 \cdot 10^{ - 6} \;{\rm{V}}^2 /{\rm{Hz}}}}\hspace{0.15cm}\underline{ = 4}.$$

MF output $d_{\rm S}(t)$ for subtask (5)

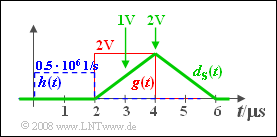
(5) The matched filter output pulse $d_{\rm S}(t)$ is triangular between $2 \hspace{0.05cm}\rm µ s$ and $6 \hspace{0.05cm}\rm µ s$.

The maximum $g_0\hspace{0.15cm}\underline{= 2 \hspace{0.08cm}\rm V}$ is at $T_\text{D, opt} =4 \hspace{0.05cm}\rm µ s$.
The noise power is given by:

$$\sigma _d ^2 = \frac{N_0 }{2 \cdot \Delta t_h } \hspace{0.15 cm}\underline{= 1\;{\rm{V}}^2} .$$

Using these two quantities, we can calculate the maximum S/N ratio:

$$\rho _d (T_{{\rm{D, \hspace{0.08cm}opt}}} ) = \frac{{d_{\rm S} (T_{{\rm{D, \hspace{0.05cm}opt}}} )^2}}{\sigma _d ^2 } = \frac{({2\;{\rm{V}})^2 }}{{1\;{\rm{V}}^2 }} = 4.$$

(6) From the above diagram, one can see that now $d_{\rm S}(T_\text{D})$ is only half as large, namely $1 \hspace{0.08cm}\rm V$.

Thus for $T_\text{D} =3 \hspace{0.08cm}\rm µ s$ the S/N ratio is smaller by a factor of $4$, i.e. $\rho _d (T_{{\rm{D}}} )\hspace{0.15 cm}\underline{=1}$.

MF output $d_{\rm S}(t)$ for subtask (7)

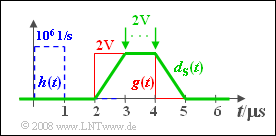
(7) Solutions 1, 3 and 4 are correct:

The diagram shows that now the output pulse $d_{\rm S}(t)$ is trapezoidal.
In the range from $3 \hspace{0.05cm}\rm µ s$ to $4 \hspace{0.05cm}\rm µ s$ the pulse $d_{\rm S}(t)$ is constantly equal to $g_0= 2 \hspace{0.08cm}\rm V$.
Because of the only half as wide impulse response $h(t)$, the frequency response $H(f)$ is more broadband by a factor of $2$ and thus the noise power is larger:

$$\sigma_d ^2 = \frac{N_0 }{2} \cdot \int_{ - \infty }^{ + \infty } {h^2 (t)\,{\rm{d}}t} = \frac{N_0 }{2 \cdot \Delta t_h } = 2\;{\rm{V}}^2 .$$

Thus, the S/N ratio is now $\rho_d (T_{{\rm{D, \hspace{0.08cm}opt}}} ) \hspace{0.15cm}\underline{= 2}.$

MF output $d_{\rm S}(t)$ for subtask (8)

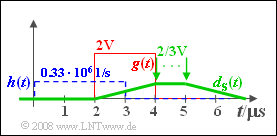
(8) Solutions 2 and 4 are correct:

The matched filter output pulse $d_{\rm S}(t)$ for $\Delta t_h = 3 \hspace{0.05cm}\rm µ s$ is sketched on the right. This is also trapezoidal.
The optimal detection time is now in the range between $4 \hspace{0.05cm}\rm µ s$ and $5 \hspace{0.05cm}\rm µ s$.
However, the useful signal $d_{\rm S}(t)$ is now only one-third as large as when matched: $d_{\rm S}(T_\text{D, opt}) = 2/3 \hspace{0.08cm}\rm V$.
For the noise power now applies:

$$\sigma_d ^2 = \frac{N_0 }{2 \cdot \Delta t_h } = \frac{2}{3}\;{\rm{V}}^2 .$$

Thus, the noise power is smaller (i.e. more favorable) than with adaptation according to subtask (5).
Nevertheless, the S/N ratio is still worse than in subtask (7) due to the smaller $d_{\rm S}(T_{\rm D})$:

$$\rho _d (T_{{\rm{D\hspace{0.15cm},opt}}} ) = \frac{{(2/3\;{\rm{V}})^2 }}{{2/3\;{\rm{V}}^2 }} = {2}/{3}.$$

	Each time point $T_{\rm D}$ in the range $3 \hspace{0.08cm}\rm µ s$ ... $4 \hspace{0.05cm}\rm µ s$ leads to the maximum SNR.
	The signal component $d_S(T_\text{D, opt})$ is smaller than calculated in subtask (5).
	The noise power $\sigma_d^2$ is larger than calculated in subtask (5).
	The S/N ratio is smaller than calculated in subtask (4).

	Each time point $T_{\rm D}$ in the range $3 \hspace{0.08cm}\rm µ s$ ... $4 \hspace{0.05cm}\rm µ s$ leads to the maximum SNR.
	The signal component $d_S(T_\text{D, opt})$ is smaller than calculated in subtask (5).
	The noise power $\sigma_d^2$ is larger than calculated in subtask (5).
	The S/N ratio is smaller than calculated in subtask (4).

	The filter is matched to the input pulse $g(t)$.
	There is another filter with larger S/N ratio.
	The filter can be implemented as an integrator over time $\Delta t_h$.