Exercise 5.7Z: Matched Filter - All Gaussian
From LNTwww
(Redirected from Aufgabe 5.7Z: Matched-Filter - alles gaußisch)
At the input of a reception filter there is
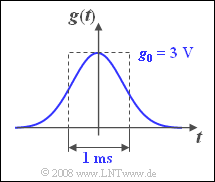
- a Gaussian pulse $g(t)$ with amplitude $g_0$ and equivalent duration $\Delta t_g = 1\hspace{0.08cm} \rm ms$,
- $$g(t) = g_0 \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {t/\Delta t_g } \right)^2 } ,$$
- superimposed by white Gaussian noise with power density $N_0 = 10^{-4}\hspace{0.08cm} \rm V^2 \hspace{-0.1cm}/Hz$.
The pulse energy is $E_g = 0.01\hspace{0.08cm} \rm V^2 s$. Let the reception filter be an acausal Gaussian low-pass filter with frequency response
- $$H_{\rm E} (f) = {\rm{e}}^{ - {\rm{\pi }}\left( {f/\Delta f_{\rm E} } \right)^2 } .$$
The associated impulse response is thus:
- $$h_{\rm E} (t) = \Delta f_{\rm E} \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta f_{\rm E} \hspace{0.03cm}\cdot \hspace{0.03cm}t} \right)^2 } .$$
The system-theoretical filter bandwidth $\Delta f_{\rm E}$ should be chosen so that the Gaussian low-pass filter is optimally matched to the input impulse $g(t)$. This is then referred to as a: "matched filter".
Notes:
- The exercise belongs to the chapter Matched Filter.
- Use the following definite integral to solve:
- $$\int_0^\infty {{\rm{e}}^{ - a^2 x^2 } {\rm{d}}x = \frac{{\sqrt {\rm{\pi }} }}{2a}} .$$
Questions
Solution
(1) For the energy of an pulse $g(t)$ applies in general, or for this example:
- $$E_g = \int_{ - \infty }^{ + \infty } {g^2(t) \hspace{0.1cm}{\rm{d}}t} = g^2_0 \cdot \int_{ - \infty }^{ + \infty } {{\rm{e}}^{ - 2{\rm{\pi }}\left( {t/\Delta t_g } \right)^2 } \hspace{0.1cm}{\rm{d}}t} .$$
- This equation can be transformed as follows:
- $$E_g = 2 \cdot g_0 ^2 \cdot \int_0^\infty {{\rm{e}}^{ - \left( {\sqrt {2 \rm{\pi }} /\Delta t_g } \right)^2 \cdot \hspace{0.05cm} t^2 }\hspace{0.1cm} {\rm{d}}t} .$$
- With $a = (2\pi)^{1/2}\cdot 1/\Delta t_g$ and the formula given, the following relationship holds:
- $$E_g = 2 \cdot g_0 ^2 \cdot \frac{{\sqrt {\rm{\pi }} }}{2a} = \sqrt 2 \cdot g_0 ^2 \cdot \Delta t_g .$$
- Solving this equation for $g_0$, the final result is:
- $$g_0 = \sqrt {\frac{E_g }{\Delta t_g \cdot \sqrt 2 }} = \sqrt {\frac{{0.01\;{\rm{V}}^{\rm{2}} {\rm{s}}}}{{0.001\;{\rm{s}} \cdot 1.414}}} \hspace{0.15cm}\underline { = 2.659\;{\rm{V}}}.$$
(2) Assuming a matched filter, the S/N ratio at the output is:
- $$\rho _{d} ( {T_{{\rm{D,}}\,{\rm{opt}}} } ) = \frac{2 \cdot E_g }{N_0 } = \frac{{2 \cdot 10^{ - 2} \;{\rm{V}}^{\rm{2}} {\rm{s}}}}{{10^{ - 4} \;{\rm{V}}^{\rm{2}} {\rm{/Hz}}}} = 200.$$
- In logarithmic representation, the following result is obtained:
- $$10 \cdot \lg \rho _{d} ( {T_{{\rm{D,}}\,{\rm{opt}}} } ) = 10 \cdot \lg \left( {200} \right) \hspace{0.15cm}\underline {\approx 23\;{\rm{dB}}}.$$
(3) A comparison between the input pulse and the filter frequency response shows that when $\Delta f_{\rm E} = 1/\Delta t_g$ is fitted, it must hold:
- $$\Delta f_{{\rm{E,}}\,{\rm{opt}}} \hspace{0.15cm}\underline { = 1\;{\rm{kHz}}}.$$
(4) Solutions 1 and 3 are correct:
- A smaller filter bandwidth is favorable with respect to interference,
- but unfavorable with respect to the useful signal.
- The negative influence (smaller useful signal) outweighs the positive influence (less noise).