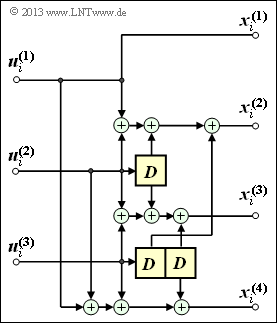
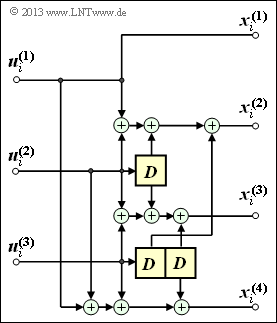
Exercise 3.1: Analysis of a Convolutional Encoder

• Return to book

Predefined convolutional encoder

We consider the outlined convolutional encoder and assume the following information sequence:

$$\underline{\it u} = \big( 0,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm}\text{...} \big )\hspace{0.05cm}.$$

This sequence is divided into three strands:

$$\underline{\it u}^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \big( 0,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm} \text{...} \big )\hspace{0.05cm},$$

$$\underline{\it u}^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \big( 1,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm}\text{...} \big )\hspace{0.05cm},$$

$$\underline{\it u}^{(3)} \hspace{-0.15cm} \ = \hspace{-0.15cm} \big( 1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm}\text{...} \big )\hspace{0.05cm}.$$

The bits present at the coder at time  $i$  are denoted by  $u_i^{\rm (1)}$,  $u_i^{\rm (2)}$  and  $u_i^{\rm (3)}$ . For example  $u_1^{\rm (1)} = 0$,  $u_2^{\rm (2)} = 1$,  $u_3^{\rm (3)} = 1$.

The purpose of this exercise is to determine

• the number  $k$  of information bits processed per coding step,

• the number  $n$  of code bits output per coding step,

• the memory order  (or, for short,  the memory)  $m$,

• the total influence length  (or for short:  influence length)  $\nu$.

For the given information sequence   $\underline {u}$   you shall determine the code symbols  $x_i^{(1)}$,  $x_i^{(2)}$,  $x_i^{(3)}$  and  $x_i^{(4)}$  for the clock instants  $i = 1$  and  $i = 3$.  It must be assumed that all memory elements were filled with zeros at the beginning.

Hints:

• This exercise refers to the chapter  "Basics of Convolutional Coding".

• For completeness,  the code bits to the clock step  $i = 2$  are also given here:

$$x_2^{(1)} = 1 \hspace{0.05cm},\hspace{0.4cm}x_2^{(2)} = 0 \hspace{0.05cm},\hspace{0.4cm} x_2^{(3)} = 0 ,\hspace{0.4cm}x_2^{(4)} = 0 \hspace{0.05cm}.$$

• However,  this last specification is not needed to solve the exercise.

Questions

1

What are the code parameters  $k$  and  $n$?

$k \ = \ $

$n \ = \ $

2

What are the memory order  $m$  and the total influence length  $\nu$?

$m \ = \ $

$\nu \ = \ $

3

What are the code bits in the first coding step  $(i = 1)$?

$x_1^{(1)} \ = \ $

$x_1^{(2)} \ = \ $

$x_1^{(3)} \ = \ $

$x_1^{(4)} \ = \ $

4

What are the codebits in the third coding step  $(i = 3)$?

$x_3^{(1)} \ = \ $

$x_3^{(2)} \ = \ $

$x_3^{(3)} \ = \ $

$x_3^{(4)} \ = \ $

Solution

Solution

(1)  At each clock,  $\underline {k = 3}$  new information bits are processed and  $\underline {n = 4}$  code bits are output.

(2)  We denote here the influence lengths of the information sequences  $\underline{u}^{(j)}$  by  $\nu_j$,  where  $1 ≤ j ≤ k = 3$  is to be set.  Then holds:

$$\nu_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0 \hspace{0.15cm}{\rm (for \hspace{0.15cm}the \hspace{0.15cm}first \hspace{0.15cm}sequence\hspace{0.15cm}no \hspace{0.15cm}shift \hspace{0.15cm}register \hspace{0.15cm}is \hspace{0.15cm}necessary)}\hspace{0.05cm},\hspace{0.2cm} \nu_2 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1\hspace{0.05cm},\hspace{0.2cm}\nu_3 = 2\hspace{0.05cm}.$$

• The memory order  $m$  $($or memory for short$)$  of the encoder is given by the longest shift register   ⇒   $\underline {m = 2}$.

• The total influence length  $($or influence length for short$)$  is equal to the number of memory elements of the entire encoder circuit   ⇒   $\underline {\nu = 3}$.

Predefined convolutional encoder

(3)  In general,  for the  $n = 4$  code bits of step  $i$:

$$x_i^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} \hspace{0.05cm},$$

$$x_i^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} + u_{i}^{(2)} + u_{i-1}^{(2)} + u_{i-1}^{(3)} \hspace{0.05cm},$$

$$x_i^{(3)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(2)} + u_{i}^{(3)}+ u_{i-1}^{(2)} + u_{i-2}^{(3)} \hspace{0.05cm},$$

$$x_i^{(4)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} + u_{i}^{(2)} + u_{i}^{(3)}+ u_{i-2}^{(3)}\hspace{0.05cm}.$$

• In the first coding step,  all memory elements are assigned zeros.

• Therefore for  $i = 1$  all bits with the indices   $i \, –1$   or   $i \, –2$   can be omitted.

• In accordance with the specification,  let further hold:   $u_1^{(1)} = 0$,  $u_1^{(2)} = 1$,  $u_1^{(3)} = 1$.

• This is obtained by modulo-2 addition:

$$x_1^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{1}^{(1)} \hspace{0.15cm}\underline {=0} \hspace{0.05cm},$$

$$x_1^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{1}^{(1)} + u_{1}^{(2)} = 0+1 \hspace{0.15cm}\underline {=1} \hspace{0.05cm},$$

$$x_1^{(3)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{1}^{(2)} + u_{1}^{(3)}= 1 + 1 \hspace{0.15cm}\underline {=0}\hspace{0.05cm},$$

$$x_1^{(4)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{1}^{(1)} + u_{1}^{(2)} + u_{1}^{(3)}= 0+1+1\hspace{0.15cm}\underline {=0}\hspace{0.05cm}.$$

(4)  In the coding step  $i = 3$  the information bits are:

$$u_i^{(1)} \hspace{-0.2cm} \ = \ \hspace{-0.2cm}1\hspace{0.05cm},\hspace{0.2cm}u_{i-1}^{(1)} = 1\hspace{0.05cm},\hspace{0.2cm}u_{i-2}^{(1)} = 0\hspace{0.05cm},$$

$$u_i^{(2)} \hspace{-0.2cm} \ = \ \hspace{-0.2cm}0\hspace{0.05cm},\hspace{0.2cm}u_{i-1}^{(2)} = 1\hspace{0.05cm},\hspace{0.2cm}u_{i-2}^{(2)} = 1\hspace{0.05cm},$$

$$u_i^{(3)} \hspace{-0.2cm} \ = \ \hspace{-0.2cm}1\hspace{0.05cm},\hspace{0.2cm}u_{i-1}^{(3)} = 0\hspace{0.05cm},\hspace{0.2cm}u_{i-2}^{(3)} = 1\hspace{0.05cm},$$

which results in the following code bits:

$$x_3^{(1)} \hspace{0.15cm}\underline {=1} \hspace{0.05cm},\hspace{0.4cm}x_3^{(2)} = 1+0+1+0\hspace{0.15cm}\underline {=0}\hspace{0.05cm},\hspace{0.4cm}x_3^{(3)}= 0+1+1+1 \hspace{0.15cm}\underline {=1} \hspace{0.05cm},\hspace{0.4cm}x_3^{(4)} = 1+0+1+1\hspace{0.15cm}\underline {=1}\hspace{0.05cm}.$$

⇒   The code bits in the coding step  $i = 2$  have already been mentioned on the information page.  Here still follows the derivation:

$$x_2^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{2}^{(1)} = 1 \hspace{0.05cm},$$

$$x_2^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{2}^{(1)} + u_{2}^{(2)} + u_{1}^{(2)} + u_{1}^{(3)} = 1+1+1+1 = 0 \hspace{0.05cm},$$

$$x_2^{(3)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{2}^{(2)} + u_{2}^{(3)}+ u_{1}^{(2)} + u_{0}^{(3)} = 1+0+1+(0) = 0\hspace{0.05cm},$$

$$x_2^{(4)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{2}^{(1)} + u_{2}^{(2)} + u_{2}^{(3)}+ u_{0}^{(3)}= 1+1+0+(0) = 0\hspace{0.05cm}.$$

• Thus,  the code sequence  $\underline {x}$  $($after multiplexing$)$  starts with  $(0100, 1000, 1011, \ \text{...})$.

• The grouping was done here only for clarity.