Exercise 1.1: ISDN Supply Lines
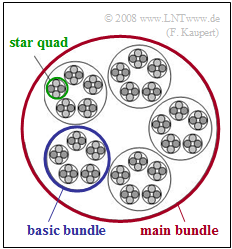
In ISDN ("Integrated Services Digital Network") the final branch (near the subscriber) is connected to a "local exchange" $\rm (LE)$ by a copper twisted pair, whereby two twisted pairs are twisted into a so-called "star quad". Several such star quads are then combined to form a "basic bundle", and several basic bundles are combined to form a "main bundle" (see graphic).
In the network of "Deutsche Telekom" (formerly: "Deutsche Bundespost"), mostly copper lines with $0.4$ mm core diameter are found, for whose attenuation and phase function the following equations are given in [PW95]:
- $$\frac{a_{\rm K}(f)}{\rm dB} = \left [ 5.1 + 14.3 \cdot \left (\frac{f}{\rm MHz}\right )^{0.59}\right ]\cdot\frac{l}{\rm km} \hspace{0.05cm},$$
- $$\frac{b_{\rm K}(f)}{\rm rad} = \left [ 32.9 \cdot \frac{f}{\rm MHz} + 2.26 \cdot \left (\frac{f}{\rm MHz}\right )^{0.5}\right ]\cdot\frac{l}{\rm km} \hspace{0.05cm}.$$
Here $l$ denotes the cable length.
Notes:
- The exercise belongs to the chapter "General Description of ISDN".
- In particular, reference is made to the section "Network infrastructure for ISDN".
- Further information on the attenuation of copper lines can be found in the chapter "Properties of Electrical Cables" of the book "Linear and Time Invariant Systems".
- [PW95] refers to the following (German language) publication: Pollakowski, P.; Wellhausen, H.-W.: Eigenschaften symmetrischer Ortsanschlusskabel im Frequenzbereich bis 30 MHz. Deutsche Telekom AG, Forschungs- und Technologiezentrum Darmstadt, 1995.
Questions
Solution
- $$\underline{N = 50}.$$
(2) Solutions 1 and 2 are correct:
- Two-wire transmission requires a directional separation method, namely the so-called "fork circuit". This has the task that at receiver $\rm A$ only the transmitted signal of subscriber $\rm B$ arrives, but not the own transmitted signal. This is generally quite successful with narrowband signals – for example, speech – but not completely.
- Due to inductive and capacitive couplings, crosstalk can occur from the twin wire located in the same star quad, whereby "near-end crosstalk" $($i.e. the interfering transmitter and the interfered receiver are located together$)$ leads to greater impairments than "far-end crosstalk".
- On the other hand, the last solution is not applicable. Intersymbol interference – i.e. the mutual interference of neighboring symbols – can certainly occur, but it is not related to two-wire transmission. The reason for this are rather (linear) distortions due to the specific attenuation and phase curves.
(3) The DC signal attenuation by a factor of $4$ can be expressed as follows:
- $$a_{\rm K}(f = 0) = 20 \cdot {\rm lg}\,\,(4) = 12.04\,{\rm dB}\hspace{0.05cm}.$$
- With the given coefficient $\text{5.1 dB/km}$, this gives the cable length $l = 12.04/5.1\hspace{0.15cm}\underline{ = 2.36 \ \rm km}$.
(4) Using the given equations and $ l = 2.36 \ \rm km$, we obtain:
- $$a_{\rm K}(f = 120\,{\rm kHz})= (5.1 + 14.3 \cdot 0.12^{\hspace{0.05cm}0.59}) \cdot 2.36\,{\rm dB} \hspace{0.15cm}\underline{\approx 21.7\,{\rm dB}}\hspace{0.05cm},$$
- $$b_{\rm K}(f = 120\,{\rm kHz}) = (32.9 \cdot 0.12 + 2.26 \cdot 0.12^{\hspace{0.05cm}0.5}) \cdot 2.36\,{\rm rad}\hspace{0.15cm}\underline{ \approx 11.2\,{\rm rad}}\hspace{0.05cm}.$$