Exercise 1.1Z: Low-Pass Filter of 1st and 2nd Order
The simplest form of a low-pass filter – for example, realisable as an RC low-pass filter according to Exercise 1.1 – has the following frequency response:
- $$H_{\rm 1}(f) = \frac{1}{1+{\rm j}\cdot f/f_0}.$$
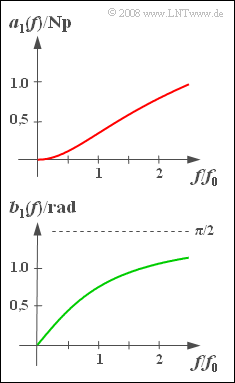
This is then referred to as a low-pass filter of first order. The diagram shows the following for this filter
- above the "damping curve" $a_1(f)$,
- below the "phase response" $b_1(f)$.
Correspondingly, for a low-pass filter of $n$–th order the following defining equation applies:
- $$H_n(f) = H_{\rm 1}(f)^n.$$
In this task,
- based on the functions $a_1(f)$ and $b_1(f)$ of the low-pass filter of first order
- the damping curve and phase response of a low-pass filter of higher order is to be analyzed.
In general, the following holds:
- $$H(f) = {\rm e}^{-a(f) - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}b(f)}.$$
Hint:
- The exercise belongs to the chapter System Description in Frequency Domain.
- There is the following relationship between the Np- and dB-values of an amplitude value $|H| = 1/x$ :
- $$a_{\rm Np} = \ln (x) = \ln (10) \cdot \lg (x) = \frac{\ln (10)}{20} \cdot a_{\rm dB} \approx 0.11513 \cdot a_{\rm dB}.$$
- Further consider that for two complex quantities $z_1$ and $z_2$ the following equations hold:
- $$|z_1 \cdot z_2| = |z_1| \cdot |z_2|, \hspace{0.5 cm}{\rm arc}\hspace{0.05 cm}(z_1 \cdot z_2) = {\rm arc}\hspace{0.05 cm}(z_1) + {\rm arc}\hspace{0.05 cm}(z_2).$$
Questions
Solution
- $$|H_{\rm 1}(f)| = \frac{1}{\sqrt{1+ (f/f_0)^2}}.$$
- This gives the damping curve in Neper (Np):
- $$a_1(f) = \ln \frac{1}{|H_1(f)|} = {1}/{2} \cdot \ln \left[1 + ({f}/{f_0})^2 \right] \Rightarrow a_1(f = f_0) = 0.3466 \hspace{0.1 cm}{\rm Np},\hspace{0.5 cm}a_1(f = 2 f_0) = 0.8047 \hspace{0.1 cm}{\rm Np}.$$
The corresponding dB values are obtained by multiplying by $1/0.11513 = 8.68589$ and result in
- $ \underline{3.01 \: {\rm dB} ≈ 3 \: {\rm dB}}$ für $ f = f_0$,
- $ \underline{6.99 \: {\rm dB}}$ für $ f = 2f_0$.
Thus, for the low-pass filter of first order the 3dB cut-off frequency is $f_{\rm G} = f_0$.
(2) The frequency response $H_1(f)$ can also be represented separately by thr real and the imaginary part:
- $$H_{\rm 1}(f) = \frac{1}{ {1+ (f/f_0)^2} } - {\rm j} \cdot \frac{f/f_0}{ {1+ (f/f_0)^2} }.$$
- Hence, the following holds for the phase response:
- $$b_1(f) = - \arctan \hspace{0.1cm} ( {\rm Im} /{\rm Re} ) = \arctan \hspace{0.1cm} ({f}/{f_0}).$$
- The value $\arctan(1) = π/4 \rm \underline{\: = 0.786 \: rad}$ is obtained for $f = f_0$ and $\arctan(2) \rm \underline{\: = 1.108 \: rad}$ for $f = 2f_0$ .
(3) For the amplitude response of a low-pass filter of $n$–th order the following is valid:
- $$|H_n(f)| = |H_{\rm 1}(f)|^n.$$
Regarding the (logarithmic) damping function the $n$–fold multiplication becomes the $n$–fold sum:
- $$a_n(f) = n \cdot a_1(f)= {n}/{2} \cdot \ln \left[ 1 + ({f}/{f_0})^2 \right].$$
For the low-pass filter of second order this results in the special case:
- $$a_2(f) = \ln \left[ 1 + ({f}/{f_0})^2 \right]= 2 \cdot a_1(f).$$
The dB values are now:
- $ \underline{6.02 \: {\rm dB} ≈ 6 \: {\rm dB}}$ für $f = ±f_0$,
- $\rm \underline{13.98 \: {\rm dB} ≈ 14 \: {\rm dB}}$ für $f = ±2f_0$.
It is thus obvious that for $n > 1$ the parameter $f_0$ no longer indicates the 3dB cut off frequency $f_{\rm G}$.
For $n = 2$ ⇒ "low-pass filter of second order" the following relationship applies instead:
- $${f_{\rm G} } = {f_0}/\sqrt{2}.$$
(4) Also, with respect to the phase function the following holds:
- $$b_n(f) = n \cdot b_1(f), \hspace{0.3 cm} b_2(f) = 2 \cdot b_1(f).$$
Thus, for the low-pass filter of second order all phase values between $±π$ are possible. In particular the following holds:
- $b_2(f = f_0) = π/2 \rm \underline{\: = 1.571 \: rad}$,
- $b_2(f = 2f_0) = \rm 2.216 \: rad$.
Since "phase" is an odd function the following applies to it: $b_2(f = \: –2f_0) = \rm \underline{–2.216 \: rad}$.