Exercise 1.1Z: Sum of Two Ternary Signals
From LNTwww
Let two three-stage message sources $X$ and $Y$ be given, whose output signals can only assume the values $-1$, $0$ and $+1$ respectively. The signal sources are statistically independent of each other.
- A simple circuit now forms the sum signal $S = X + Y$.
- At the signal source $X$, the values $-1$, $0$ and $+1$ occur with equal probability.
- For source $Y$, the signal value $0$ is twice as likely as the other two values $-1$ and $+1$, respectively.
Hints:
- The exercise belongs to the chapter Some basic definitions of probability theory.
- Solve the subtasks (3) and (4) according to the classical definition.
- Nevertheless, consider the different occurrence frequencies of the signal $Y$.
- The topic of this section is illustrated with examples in the (German language) learning video
Klassische Definition der Wahrscheinlichkeit $\Rightarrow$ "Classical definition of probability".
Questions
Solution
(1) Since the probabilities of $ \pm 1$ are the same and ${\rm Pr}(Y = 0) = 2 \cdot {\rm Pr}(Y = 1)$ holds, we get:
- $${\rm Pr}(Y = 1) + {\rm Pr}(Y = 0) + {\rm Pr}(Y = -1) = 1/2 \cdot {\rm Pr}(Y = 0) + {\rm Pr}(Y = 0) + 1/2\cdot {\rm Pr}(Y = 0) = 1\hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm Pr}(Y = 0)\;\underline { = 0.5}. $$
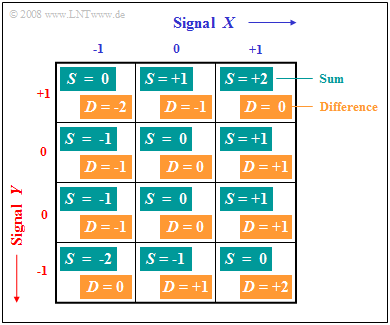
(2) $S$ can take a total of $\underline {I =5}$ values, namely $0$, $\pm 1$ and $\pm 2$.
(3) Since $Y$ is not equally distributed, one cannot (actually) apply the "Classical Definition of Probability" here.
- However, if we divide $Y$ into four ranges according to the graph, assigning two of the ranges to the event $Y = 0$, we can still proceed according to the classical definition.
- One then obtains:
- $${\rm Pr}(S = 0) = {4}/{12} = {1}/{3},$$
- $${\rm Pr}(S = +1) = {\rm Pr}(S = -1) ={3}/{12} = {1}/{4},$$
- $${\rm Pr}(S = +2) = {\rm Pr}(S = -2) ={1}/{12}$$
- $$\Rightarrow \hspace{0.3cm}{\rm Pr}(S = S_{\rm max}) = {\rm Pr}(S = +2) =1/12 \;\underline {= 0.0833}.$$
(4) It is also evident from the graph that the difference signal $D$ and the sum signal $S$ take the same values with equal probabilities.
- This was to be expected, since ${\rm Pr}(Y = +1) ={\rm Pr}(Y = -1)$ is given ⇒ Proposed solution 1.