Exercise 1.4: Low-Pass Filter of 2nd Order

Low-pass filter of first order (top)
and of second order (bottom)

In Exercise 1.1 and Exercise 1.1Z of the chapter System Description in Frequency Domain the so-called "RC low-pass filters" were described in the frequency domain. Now, the time domain representation is elaborated on.

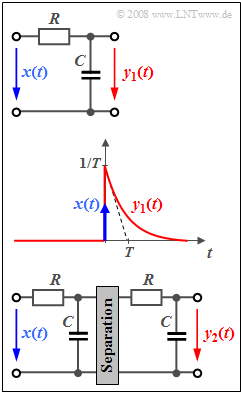
The circuit with the input signal $x(t)$ and the output signal $y_1(t)$ is a low-pass filter of first order with frequency response

$$H_{\rm 1}(f) = \frac{1}{1+{\rm j}\cdot f/f_{\rm 0}}.$$

Here, $f_0 = 1/(2πRC)$ indicates the 3dB cut-off frequency. If a Dirac-shaped signal $x(t) = δ(t)$ is applied to the input, the signal $y_1(t)$ is given by the system output according to the sketch in the middle.

The relationship between the system parameters $R$ (resistance), $C$ (capacitance) and $T$ is (see Exercise 1.3Z):

$$T = \frac{1}{\omega_{\rm 0}}= \frac{1}{2\pi f_{\rm 0}} = R \cdot C.$$

For numerical calculations $T = 1 \ \rm ms$ shall be used in the following.

The circuit below with input $x(t)$ and output $y_2(t)$ represents a low-pass filter of second order:

$$H_{\rm 2}(f) = \big[H_{\rm 1}(f)\big]^2 =\frac{1}{(1+{\rm j}\cdot f/f_{\rm 0})^2}.$$

The impulse response associated with $H_2(f)$ is $h_2(t)$.
The system parameter $f_0$ no longer indicates the 3dB cut-off frequency for a low-pass filter of second or higher order.
Furthermore, it should be noted that the two RC elements must be decoupled in order to achieve impedance matching.
An operational amplifier, for example, is suitable for this. However, this hint is not relevant for the solution of this task.

Please note:

The exercise belongs to the chapter System Description in Time Domain.
The following indefinite integral is given:

$$\int u \cdot {\rm e}^{a \cdot \hspace{0.03cm} u} \hspace{0.1cm}{\rm d}u = \frac{{\rm e}^{\hspace{0.03cm}a \cdot \hspace{0.03cm} u}}{a^2} \cdot (a \cdot u -1).$$

Questions

$t_1\ = \ $

$\ \rm ms$

$y_1(t = 0) \ = \ $

$y_1(t = T) \ = \ $

$t_2 \ = \ $

$\rm ms$

$h_2(t = t_2) \ = \ $

$\rm 1/s$

$y_2(t = T) \ = \ $

$\rm V$

$y_2(t = 5T) \ = \ $

$\rm V$

Solution

(1) By definition the impulse response is equal to the output signal if a Dirac delta function of weight $1$ is applied to the input.

According to the solution of Exercise 1.3Z and the sketch above the following holds:

$$h_1(t) = y_1(t) ={1}/{T} \cdot {\rm e}^{-t/T}.$$

For the time $t_1$ the following shall hold:

$$h_1(t_{\rm 1}) ={1}/{T} \cdot {\rm e}^{-t_{\rm 1}/T} = \frac{1}{2T} \hspace{0.5cm}\Rightarrow\hspace{0.5cm}{t_{\rm 1}}/{T} = {\rm ln}(2)\hspace{0.1cm} \Rightarrow \hspace{0.1cm}t_{\rm 1} = 0.693 \cdot T \hspace{0.15cm}\underline{= {\rm 0.693\,\,ms}}.$$

(2) The input signal $x(t)$ is an exponentially decreasing impulse like the impulse response $h_1(t)$ but dimensionless.

Illustration of the convolution

Thus, according to the convolution theorem:

$$y_1(t) = x (t) * h_1 (t) = T \cdot \big[ h_1 (t) * h_1 (t) \big].$$

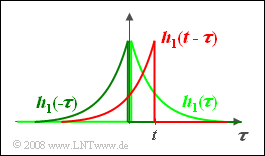
The convolution is illustrated here for a specific time $t$ by a sketch.

The following is obtained after renaming the variables:

$$\begin{align*}h_1(\tau) & = \frac{1}{T} \cdot {\rm e}^{-\tau/T}\hspace{0.1cm} \Rightarrow \hspace{0.1cm}h_1(-\tau) = \frac{1}{T} \cdot {\rm e}^{\tau/T}\hspace{0.1cm} \Rightarrow \hspace{0.1cm}h_1(t-\tau) = \frac{1}{T} \cdot {\rm e}^{(-t+\tau)/T} \\ & \Rightarrow\hspace{0.5cm} y_1(t) = T \cdot \int\limits_{ - \infty }^{ + \infty } h_1 ( {t - \tau } )\cdot {h_1 ( \tau )} \hspace{0.1cm}{\rm d}\tau.\end{align*}$$

For $τ < 0$ the impulse response is $h_1(τ) = 0$. For $τ > t$ the first convolution operand vanishes (see sketch). From this it follows that:

$$y_1(t) = T \cdot \frac{1}{T^2}\cdot \int_{ 0 }^{ t } {\rm e}^{(-t+\tau)/T} \cdot {\rm e}^{-\tau/T} \hspace{0.1cm}{\rm d}\tau = \frac{1}{T}\cdot \int_{ 0 }^{ t } {\rm e}^{-t/T} \hspace{0.1cm}{\rm d}\tau .$$

Now, it can be observed that the integrand is independent of the integration variable $τ$. Consequently, the following holds:

$$y_1(t) = {t}/{T} \cdot {\rm e}^{-t/T}\hspace{0.1cm} \Rightarrow \hspace{0.1cm} y_1(t =0) \hspace{0.15cm}\underline{=0}; \hspace{0.5cm}y_1(t =T)={\rm e}^{-1} \hspace{0.15cm}\underline{=0.368}.$$

(3) Due to the interrelationship $H_2(f) = H_1(f) · H_1(f)$ the following holds for the impulse response: $h_2(t) = h_1 (t) * h_1 (t).$

Except for the additional constant factor $1/T$ the same result as in subtask (2) is obtained:

$$h_2(t) ={t}/{T^2} \cdot {\rm e}^{-t/T}.$$

The maximum value is obtained by setting the derivative to zero:

$$\frac{{\rm d} h_2(t)}{{\rm d}t} = \frac{1}{T^2} \cdot {\rm e}^{-t/T} \cdot \left( 1 - {t}/{T}\right) = 0 \hspace{0.5cm} \Rightarrow \hspace{0.5cm} t_{\rm 2} \hspace{0.15cm}\underline{= T = 1\,\,{\rm ms}} \hspace{0.5cm}\Rightarrow \hspace{0.5cm} h_2(t_{\rm 2}) =\frac{{\rm e}^{-1}}{T} =\frac{0.368}{1\,\,{\rm ms}} \hspace{0.15cm}\underline{ = {\rm 368 \hspace{0.1cm} 1/s}}.$$

(4) In general or with the result from (3) the following applies to the step response:

$${\rm \sigma_2}(t) = \int_{ 0 }^{ t } {h_2 ( \tau )} \hspace{0.1cm}{\rm d}\tau = \frac{1}{T^2} \cdot \int_{ 0 }^{ t } \tau \cdot {\rm e}^{-\tau/T} \hspace{0.1cm}{\rm d}\tau .$$

With the substitution $u = τ/T$ and using the given integral it follows that:

$${\rm \sigma_2}(t) = \int_{ 0 }^{ t /T} u \cdot {\rm e}^{-u} \hspace{0.1cm}{\rm d}u ={\rm e}^{-u} \cdot (-u-1) |_{ 0 }^{ t /T} \hspace{0.5cm} \Rightarrow \hspace{0.5cm}{\rm \sigma_2}(t) = 1- \left( 1 + {t}/{T} \right) \cdot {\rm e}^{-t/T}.$$

The following is obtained at the given times taking the factor $2\ \rm V$ further into account:

$$y_2(t = T) = {\rm 2 \,V} \cdot \left( 1- 2 \cdot {\rm e}^{-1} \right) \hspace{0.15cm}\underline{= {\rm 0.528 \,V}}, \hspace{0.9cm}y_2(t = 5T) = {\rm 2 \,V} \cdot \left( 1- 6 \cdot {\rm e}^{-5} \right) \hspace{0.15cm}\underline{= {\rm 1.919 \,V}}.$$

For even larger times $y_2(t)$ approaches more and more the final value $2\hspace{0.05cm} \rm V$ .