Exercise 1.4: Maximum Likelihood Decision
From LNTwww
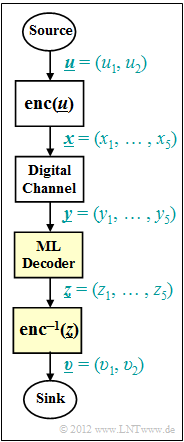
We consider the digital transmission system according to the graph. Considered are:
- a systematic $(5, 2)$ block code $\mathcal{C}$ with the code words
- $$\underline{x}_{0} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (0, 0, 0, 0, 0) \hspace{0.05cm},$$ $$\underline{x}_{1} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (0, 1, 0, 1, 0) \hspace{0.05cm},$$ $$\underline{x}_{2} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (1, 0, 1, 0, 1) \hspace{0.05cm},$$ $$\underline{x}_{3} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (1, 1, 1, 1, 1) \hspace{0.05cm};$$
- a digital (binary) channel model that changes the vector $\underline{x} \in {\rm GF} (2^{5})$ over into the vector $\underline{y} \in {\rm GF} (2^{5})$,
- a Maximum likelihood decoder (short: ML decoder) with the decision rule
- $$\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} {\rm Pr}( \underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm}|\hspace{0.05cm} \underline{y} ) = {\rm arg} \min_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i}).$$
Here, $d_{\rm H} (\underline{y}, \ \underline{x_{i}})$ is the Hamming distance between the received word $\underline{y}$ and the (possibly) sent code word $\underline{x_{i}}$.
Note: This exercise belongs to the chapter "Channel Models and Decision Structures".
Questions
Solution
(1) Correct answer 3 ⇒ $\underline{z} = \underline{x}_{2} = (1, 0, 1, 0, 1)$:
- The Hamming distances between the specific received word $\underline{y} = (1, 0, 0, 0, 1)$ and the four possible code words $\underline{x}_{i}$ are as follows:
- $$d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_0) = 2\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_1) = 4\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_2) = 1\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_3) = 3\hspace{0.05cm}.$$
- A decision is made for the sequence with the smallest Hamming distance $d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_2) = 1$.
(2) For $\underline{y} = (0, 0, 0, 1, 0)$ the answers 1 and 2 are correct, as the following calculation shows:
- $$d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_0) = 1\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_1) = 1\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_2) = 4\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_3) = 4\hspace{0.05cm}.$$
(3) Correct answer 3 ⇒ $\underline{z} = \underline{x}_{2} = (1, 0, 1, 0, 1)$:
- According to the Hamming distance, a decision in favor of $x_{2}$ would be just as possible as for $x_{3}$ if the vector $\underline{y} = (1, 0, 1, 1, 1)$ is received:
- $$d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_0) = 4\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_1) = 4\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_2) = 1\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_3) = 1\hspace{0.05cm}.$$
- But the received vector $\underline{y}$ is different from $x_{2}$ with respect to the fourth bit and from $x_{3}$ in the second bit.
- Since the fourth bit is more uncertain than the second, it will choose $x_{2}$ .
(4) Since this is a systematic code, the decision for $\underline{z} = (1, 0, 1, 0, 1)$ is equivalent to the decision
- $$v_{1} \ \underline{ = 1}, \ v_{2} \ \underline{= 0}.$$
- It is not certain that $\underline{u} = (1, 0)$ was actually sent.
- But the probability is highest for this given the received vector $\underline{y} = (1, 0, 1, 1, 1)$.