Exercise 1.7Z: BARBARA Generator

$\rm BARBARA$ Generator

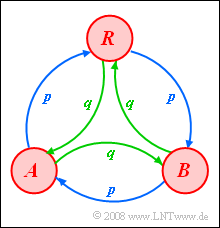
Here we consider a ternary random generator with symbols $A$, $B$ and $R$, which can be described by a homogeneous and stationary first order Markov chain.

The transition probabilities can be taken from the sketched Markov diagram.
For the first three subtasks, $p = 1/4$ should always hold.

Hints:

The exercise belongs to the chapter Markov Chains.

Questions

	The values of $p > 0$ and $q < 1$ are largely arbitrary.
	For the transition probabilities, the following must hold: $p + q = 1$.
	All symbols have equal ergodic probabilities.
	It holds here: ${\rm Pr}(A) = 1/2, \; {\rm Pr}(B) = 1/3, \; {\rm Pr}(R) = 1/6$.

$p_{\rm A} \ = \ $

$\ \cdot 10^{-3}$

$p_{\rm B} \ = \ $

$\ \cdot 10^{-3}$

$p_{\rm C} \ = \ $

$\ \cdot 10^{-3}$

${\rm Pr}(\rm BARBARA)\ = \ $

$\ \cdot 10^{-3}$

$p_{\rm opt} \ = \ $

$p = p_{\rm opt}\hspace{-0.1cm}: \hspace{0.3cm}{\rm Pr}(\rm BARBARA)\ = \ $

$\ \cdot 10^{-3}$

Musterlösung

Solution

(1) Correct are the second and third suggested solutions:

The sum of all outgoing arrows must always be $1$. Therefore $q = 1 - p$ holds.
Because of the symmetry of the Markov diagram, the ergodic probabilities are all equal:

$${\rm Pr}(A) ={\rm Pr}(B) ={\rm Pr}(R) = 1/3.$$

(2) If one is in the state $B$ at the starting time $\nu=0$, because of ${\rm Pr}(B\hspace{0.05cm}|\hspace{0.05cm}B) = 0$ the state $B$ is not possible at time $\nu=1$.

One fails here already with the initial letter $B$:

$$p_{\rm B} \; \underline{ =0}.$$

For the calculation of $p_{\rm A}$ it should be noted: Starting from $A$ one goes in the Markov diagram first to $B$ $($with probability $q)$, then five times clockwise $($each time with probability $p)$ and finally from $R$ to $A$ $($with probability $q)$. Meaning:

$$p_{\rm A} = q^2 \hspace{0.05cm}\cdot \hspace{0.05cm} p^5 = 3^2 / 4^7 \hspace{0.15cm}\underline {\approx 0.549 \hspace{0.05cm}\cdot \hspace{0.05cm} 10^{-3}}.$$

In a similar way, one obtains:

$$p_{\rm R} = q \hspace{0.05cm}\cdot \hspace{0.05cm} p^6 = 3 / 4^7 \hspace{0.15cm}\underline {\approx 0.183 \hspace{0.05cm}\cdot \hspace{0.05cm} 10^{-3}}.$$

(3) By averaging over the conditional probabilities we obtain:

$${\rm Pr}(\rm BARBARA) = p_{\rm A} \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm Pr}(A) \hspace{0.1cm} + \hspace{0.1cm}p_{\rm B} \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm Pr}(B) \hspace{0.1cm} + \hspace{0.1cm}p_{\rm R} \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm Pr}(R).$$

This leads to the result:

$${\rm Pr}(\rm BARBARA) = {1}/{3} \cdot \left( q^2 \hspace{0.05cm}\cdot \hspace{0.05cm} p^5 \hspace{0.1cm} +\hspace{0.1cm}0 \hspace{0.1cm} +\hspace{0.1cm}q \hspace{0.05cm}\cdot \hspace{0.05cm} p^6 \right) = \frac{q \hspace{0.05cm}\cdot \hspace{0.05cm} p^5 }{3} \cdot{p+q} = \hspace{-0.15cm} \frac{q \hspace{0.05cm}\cdot \hspace{0.05cm} p^5 }{3} \hspace{0.15cm}\underline { \approx 0.244 \hspace{0.05cm}\cdot \hspace{0.05cm} 10^{-3}}.$$

(4) The probability calculated in (3) is $p^5 \cdot (1-p)/3$, where $q= 1-p$ is considered.

By setting the differential to zero, we obtain the governing equation:

$$5 \cdot p^4 - 6 \cdot p^5 = 0 \hspace{0.5cm} \Rightarrow \hspace{0.5cm} p_{\rm opt} = 5/6 \hspace{0.15cm}\underline { \approx \rm 0.833}.$$

This results in a value that is larger than the subtask (3) by a factor $90$ approximately:

$${\rm Pr}\rm (BARBARA) \hspace{0.15cm}\underline { \approx 22 \hspace{0.05cm}\cdot \hspace{0.05cm} 10^{-3}}.$$