Exercise 2.07: Reed-Solomon Code (7, 3, 5) to Base 8

$\rm GF(2^3)$ representation as powers, polynomials, vectors

The Reed–Solomon code considered here, denoted $\rm RSC \, (7, \, 3, \, 5)_8$,

encodes a block of information $\underline{u} = (u_0, \, u_1, \, u_2)$ of $k = 3$ symbols, where $u_0, \, u_1, \, u_2 ∈ \rm GF(2^3)$ applies, representing symbols rather than bits;

generates a code word $\underline{c} = (c_0, \, c_1,\hspace{0.05cm} \text{...} \hspace{0.1cm} , c_6)$ of length $n = 7$ with code symbols $c_i$ also from the Galois field $\rm GF(2^3)$;

has the free distance $d_{\rm min} = n - k + 1 = 5$, so that up to $e = 4$ symbol errors can be detected and up to $t = 2$ symbol errors can be corrected.

The elements of the underlying Galois field are:

$${\rm GF}(2^3) = \{\hspace{0.1cm} 0\hspace{0.05cm},\hspace{0.1cm} 1 \hspace{0.05cm},\hspace{0.1cm} \alpha\hspace{0.05cm},\hspace{0.1cm} \alpha^{2} \hspace{0.05cm},\hspace{0.1cm} \alpha^{3} \hspace{0.05cm},\hspace{0.1cm} \alpha^{4} \hspace{0.05cm},\hspace{0.1cm} \alpha^{5} \hspace{0.05cm},\hspace{0.1cm} \alpha^{6} \hspace{0.1cm}\}\hspace{0.05cm}. $$

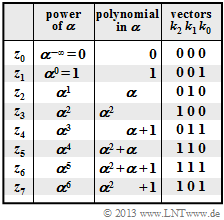
These elements can also be represented as polynomials or as coefficient vectors according to the graphic.

One can see from the above table that all $u_i ∈ \rm GF(2^3)$ and all $c_i ∈ \rm GF(2^3)$ can also be characterized by $m = 3 \ \ \rm bits$, for example $\alpha^4$ by "$110$".
In this exercise, you are to trace the encoding process for the binary input sequence

$$110 \hspace{0.09cm}001\hspace{0.09cm} 011\hspace{0.09cm} 000\hspace{0.09cm} 000\hspace{0.09cm} 000\hspace{0.09cm} 111 \hspace{0.05cm} \text{...} $$

Note that:

The Reed–Solomon coder works blockwise. In the first coding step, the code symbols $c_0, \hspace{0.05cm} \text{...} \hspace{0.1cm} , c_6$ are generated, then in the second step from the information block $\underline{u} = (u_3, \, u_4, \, u_5)$ the symbols $(c_7, \hspace{0.05cm} \text{...} \hspace{0.1cm} , c_{13})$ of the second code word, etc.
One describes the information block $\underline{u}$ by the polynomial $u(x) = u_0 + u_1 \cdot x + u_2 \cdot x^2$ of degree $2$. In general, for the Galois field $\rm GF(2^m)$ the degree of the polynomial results to $m - 1$.
The code symbols $c_0, \hspace{0.05cm} \text{...} \hspace{0.1cm} , c_6$ are obtained by substituting into the polynomial $u(x)$ for the parameter $x$ all elements of $\rm GF(2^3)$ except the zero element:

$${\rm GF}(2^3)\hspace{-0.01cm}\setminus \hspace{-0.01cm}\{ 0\} = \{\hspace{0.1cm}\alpha^{0}\hspace{0.05cm},\hspace{0.1cm} \alpha^1\hspace{0.05cm},\hspace{0.1cm} \alpha^{2} \hspace{0.05cm},\hspace{0.1cm} \alpha^{3} \hspace{0.05cm},\hspace{0.1cm} \alpha^{4} \hspace{0.05cm},\hspace{0.1cm} \alpha^{5} \hspace{0.05cm},\hspace{0.1cm} \alpha^{6} \hspace{0.1cm}\}\hspace{0.05cm}. $$

Formally, the $\rm RSC \, (7, \, 3, \, 5)_8$ can be described as follows:

$$C_{\rm RS} = \Big \{ \underline {c} = \big ( u(\alpha^{0}) \hspace{0.05cm},\hspace{0.1cm} u(\alpha^{1})\hspace{0.05cm},\hspace{0.1cm}u(\alpha^{2})\hspace{0.1cm} \big ) \hspace{0.1cm} \big | \hspace{0.2cm} u(x) = \sum_{i = 0}^{2} u_i \cdot x^{i}\hspace{0.05cm},\hspace{0.2cm} u_i \in {\rm GF}(2^3) \Big \} \hspace{0.05cm}.$$

Hints:

This exercise belongs to the chapter "Definition and Properties of Reed–Solomon Codes".

The "Exercise 2.8" is structured similarly to this one, but the generator matrix $\mathbf{G}$ is then used to generate a code word $\underline{c}$.

Questions

Solution

(1) Correct is the proposed solution 2:

All information symbols here come from the Galois field $\rm GF(2^3)$. In binary notation, each symbol is represented by three bits.

Because of the Reed-Solomon code parameter $k = 3$, an information block consists of three information symbols: $\underline{u} = (u_0, \, u_1, \, u_2)$.

Accordingly, the binary information block $\underline{u}_{\rm bin}$ contains exactly $3 \cdot 3 = 9$ bits.

(2) According to the table on the information page, there is the following relationship between the coefficient vector and the exponential representation:

$$(110) \hspace{0.1cm} \Rightarrow \hspace{0.2cm} u_0 = \alpha^{4}\hspace{0.05cm},\hspace{0.6cm} (001) \hspace{0.1cm} \Rightarrow \hspace{0.2cm} u_1 = \alpha^{0} = 1\hspace{0.05cm},\hspace{0.6cm} (011) \hspace{0.1cm} \Rightarrow \hspace{0.2cm} u_2 = \alpha^{3}\hspace{0.05cm}. $$

Correct are the proposed solutions 1, 4, and 5.

The information block in the first coding step is $\underline{u} = (\alpha^4, \, 1, \, \alpha^3)$.

(3) In polynomial representation, the information block $\underline{u} = (\alpha^4, \, 1, \, \alpha^3)$ results in:

$$u(x) = u_0 + u_1 \cdot x + u_2 \cdot x^2 = \alpha^{4} + x + \alpha^{3}\cdot x^2 \hspace{0.05cm}. $$

Therefore the proposed solution 3 is correct.

The first proposed solution cannot be correct, since the polynomial degree can be at most $2$, if all information and code symbols originate from $\rm GF(2^3)$.

(4) For the code symbols you get with the polynomial representation according to the specification page:

$$c_0 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u(x = \alpha^{0} = 1) = \alpha^{4} + 1 + \alpha^{3}\cdot 1^2 = (110) + (001) + (011)= (100) = \alpha^{2} \hspace{0.05cm},$$

$$c_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u(x = \alpha^{1}) = \alpha^{4} + \alpha + \alpha^{5}= (110) + (010) + (111) = (011) = \alpha^{3} \hspace{0.05cm},$$

$$c_2 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u(x = \alpha^{2}) = \alpha^{4} + \alpha^{2} + \alpha^{7}= (110) + (100) + (001) = (011) = \alpha^{3} \hspace{0.05cm},$$

$$c_3 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u(x = \alpha^{3}) = \alpha^{4} + \alpha^{3} + \alpha^{9}= (110) + (011) + (100) = (001) = 1 \hspace{0.05cm},$$

$$c_4 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u(x = \alpha^{4}) = \alpha^{4} + \alpha^{4} + \alpha^{11} = \alpha^{4} \hspace{0.05cm},$$

$$c_5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u(x = \alpha^{5}) = \alpha^{4} + \alpha^{5} + \alpha^{13}= (110) + (111) + (101) = (100) = \alpha^{2} \hspace{0.05cm},$$

$$c_6 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u(x = \alpha^{6}) = \alpha^{4} + \alpha^{6} + \alpha^{15}= (\alpha^{2} + \alpha) + (\alpha^2 +1) + \alpha = 1 \hspace{0.05cm}.$$

So, correct are the proposed solutions 1, 2, 3, 4, 7.

The solutions to 5 and 6 are exactly reversed.

(5) The first proposed solution is correct:

This results from the result of the subtask (4) and the assignment

$$\alpha^2 ↔ 100, \ \alpha^3 ↔ 011, \ \alpha^3 ↔ 011, \ 1 ↔ 001, \ \alpha^4 ↔ 110, \ \alpha^2 ↔ 100, \ 1 ↔ 001. $$

The last proposed solution cannot be correct, since the binary code word must consist of $n \cdot m = 7 \cdot 3 = 21$ bits.

Even if you have determined only the result $c_0 = \alpha^2$ in the subtask (4), you already know that the second answer cannot be correct.

(6) The statements 1, 3, 4 are correct:

The bits 10, ... , 18 of the input sequence are all $0$ and thus also the information symbols $u_0, \ u_1, \ u_2 ∈ \rm GF(2^3)$.

Correspondingly, $u(x) = 0$, so that all code symbols $c_i = u(x = \alpha^i)$ correspond to the zero symbol $($index: $0 ≤ i ≤ 6)$.

The binary code sequence thus consists of $n \cdot m = 21$ "zeros".

	$u_0 = \alpha^4$,
	$u_0 = 0$,
	$u_1 = \alpha^6$,
	$u_1 = \alpha^0$,
	$u_2 = \alpha^3$,
	$u_2 = \alpha^2$.

	$c_0 = \alpha^2$,
	$c_1 = \alpha^3$,
	$c_2 = \alpha^3$,
	$c_3 = 1$,
	$c_4 = \alpha^2$,
	$c_5 = \alpha^4$,
	$c_6 = 1$.

	It holds $u_0 = u_1 = u_2 = 0$.
	It holds $u(x) = 1$.
	The code word $\underline{c} ∈ \rm GF(2^3)$ consists of seven zero symbols.
	The binary code word $\underline{c}_{\rm bin} ∈ \rm GF(2)$ consists of $21$ zeros.

	$\underline{u}_{\rm bin} = (110)$,
	$\underline{u}_{\rm bin} = (110_\|001_\|011)$,
	$\underline{u}_{\rm bin} = (110_\|001_\|0)$.

	$u(x) = \alpha^3 \cdot x + x^2 + \alpha^4 \cdot x^3$,
	$u(x) = \alpha^3 + x + \alpha^4 \cdot x^2$,
	$u(x) = \alpha^4 + x + \alpha^3 \cdot x^2$.

	$\underline{c}_{\rm bin} = 100_\|011_\|011_\|001_\|110_\|100_\|001$,
	$\underline{c}_{\rm bin} = 011_\|011_\|001_\|110_\|100_\|001_\|100$,
	$\underline{c}_{\rm bin} = 100_\|111_\|0$.