Exercise 2.08Z: Addition and Multiplication in GF(2 power 3)

• Return to book

$\rm GF(2^3)$:  Incomplete addition and multiplication tables

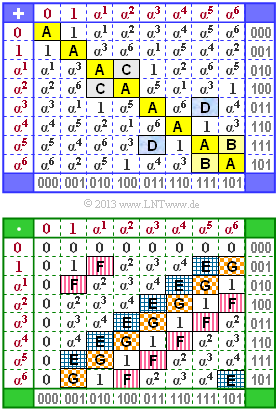
The graph shows the addition and multiplication table for the finite field  $\rm GF(2^3)$.  The tables are not complete.  Some fields  $($highlighted in color$)$  should be completed.

The elements are given both

• in the exponent representation  $($with red lettering,  left and above$)$ and

• in the coefficient representation  (gray lettering,  right and below). 

From this assignment one can already recognize the underlying irreducible polynomial  $p(\alpha)$.

• Additions  $($and subtractions$)$  are best done in the coefficient representation  $($or with polynomials firmly linked to it$)$.

• For multiplications,  however,  the exponential representation is more convenient.

Hints:

• This exercise belongs to the chapter  "Definition and Properties of Reed-Solomon Codes".

• However,  reference is also made to the chapter  "Extension Field".

Questions

1

What element does the  "$\rm A$"  stand for in the addition table?

	$\rm A = 0$,
	$\rm A = 1$,
	$\rm A = \alpha^1$,

2

What element does the  "$\rm B$"  stand for in the addition table?

	$\rm B = 0$,
	$\rm B = 1$,
	$\rm B = \alpha^1$.

3

What element does the  "$\rm C$"  stand for in the addition table?

	$\rm C = \alpha^2$,
	$\rm C = \alpha^3$,
	$\rm C = \alpha^4$.

4

What element does the  "$\rm D$"  stand for in the addition table?

	$\rm D = \alpha^2$,
	$\rm D = \alpha^3$,
	$\rm D = \alpha^4$.

5

What assignments apply in the multiplication table?

	$\rm E = \alpha^5$,
	$\rm F = \alpha^1$,
	$\rm G = \alpha^6$.

6

What irreducible polynomial underlies these tables?

	$p(\alpha) = \alpha^2 + \alpha + 1$,
	$p(\alpha) = \alpha^3 + \alpha^2 + 1$,
	$p(\alpha) = \alpha^3 + \alpha + 1$.

Solution

Solution

(1)  Adding any element of an extension field based on  $\rm GF(2)$  to itself always yields  $0$,  as can be easily seen from the coefficient representation,  for example:

$$\alpha^3 + \alpha^3 = (011) + (011) = (000) = 0 \hspace{0.05cm}.$$

• That is:   $\rm A$  stands for the zero element   ⇒   Solution 1.

(2)  $\rm B$  is the result of adding  $\alpha^5$  and  $\alpha^6$   ⇒   Solution 3:

$$\alpha^5 + \alpha^6 = (111) + (101) = (010) = \alpha^1 \hspace{0.05cm}.$$

• One could have found this result more simply,  since in each row and column each element occurs exactly once.

• After  $\rm A = 0$   is fixed,  exactly only the element  $\alpha^1$   is missing in the last row and the last column.

(3)  $\rm C$  is the result of the sum $\alpha^1 +\alpha^2$   ⇒   Solution 3:

$$\alpha^1 + \alpha^2 = (010) + (100) = (110) = \alpha^4 \hspace{0.05cm}.$$

(4)  $\rm D$  is the result of  $\alpha^3$  and  $\alpha^5$   ⇒   Solution 1:

$$\alpha^3 + \alpha^5 = (011) + (111) = (100) = \alpha^2 \hspace{0.05cm}.$$

(5)  All proposed solutions  are correct,  as can be seen from row 2  (multiplication with the  "identity element"):

$\rm GF(2^3)$:  Complete addition and multiplication tables

• The complete tables for addition and multiplication are shown opposite.

• Because of the validity of  $\alpha^i \cdot \alpha^j = \alpha^{(i+j)\hspace{0.1cm} {\rm mod}\hspace{0.1cm} 7}$,  multiplication yields a symmetry that could be used to solve.

(6)  Correct here is the  proposed solution 3:

• All polynomials are indeed irreducible.  However,  one needs a degree-3 polynomial for  $\rm GF(2^3)$.

• The third proposed solution results from the relation

$$\alpha^3 = \alpha + 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p(\alpha) = \alpha^3 + \alpha + 1 = 0 \hspace{0.05cm}.$$