Exercise 2.10: Reed-Solomon Error Detection
For a linear block code, up to $e = d_{\rm min} - 1$ errors can be detected. For all Reed–Solomon codes the minimum distance is
- $$d_{\rm min} = n-k+1 \hspace{0.05cm}.$$
One must distinguish the following cases:
- If no more than $e = d_{\rm min} - 1= n - k$ symbol errors occur, the block is always detected as faulty.
- Error detection can still work even if more than $n - k$ symbol errors occur. This is when the received word is not a valid code word of the Reed–Solomon code:
- $$\underline {y} \notin C_{\rm RS} = \{ \underline {c}_{\hspace{0.05cm}0}, \hspace{0.05cm}\text{...} \hspace{0.1cm}, \underline {c}_i, \hspace{0.05cm}\text{...} \hspace{0.1cm}, \underline {c}_{\hspace{0.05cm}n -1} \} \hspace{0.05cm}. $$
- However, if the falsified received word $(\underline{y} ≠ \underline{c})$ is a valid code word $(\underline{y\in C_{\rm RS}})$, the decoding process will leave the falsified block undetected.
We define as block error probability:
- $${\rm Pr}({\rm block\hspace{0.15cm}error}) = {\rm Pr}(\underline {y} \ne \underline {c}) \hspace{0.05cm}.$$
In this exercise, this probability is to be determined for the following codes:
- Reed–Solomon code $(7, \, 3, \, 5)_8 \ \Rightarrow \ d_{\rm min} = 5$,
- Reed–Solomon code $(7, \, 5, \, 3)_8 \ \Rightarrow \ d_{\rm min} = 3$.
Furthermore, let it hold:
- Each symbol is falsified into another symbol with probability $\varepsilon_{\rm S} = 0.1$ and correctly transferred with probability $1 - \varepsilon_{\rm S} = 0.9$.
- For the distance spectrum of a Reed–Solomon code of length $n$ holds with $d = d_{\rm min}$:
- $$W_i = {n \choose i} \cdot \sum_{j = 0}^{i-d}\hspace{0.15cm}(-1)^j \cdot {i \choose j} \cdot \big [\hspace{0.03cm}q^{i\hspace{0.03cm}-\hspace{0.03cm}j\hspace{0.03cm}-\hspace{0.03cm}d\hspace{0.03cm}+\hspace{0.03cm}1}-1 \hspace{0.03cm} \big ]\hspace{0.05cm}.$$
Besides, two bounds for the block error probability will be considered and evaluated:
- If alone the minimum distance is known, one can derive an "upper bound" from it. The weight enumerating factors $W_i$ are to be chosen in such a way, that certainly (that is: with all constellations) applies:
- $${\rm Pr}({\rm upper\hspace{0.15cm} bound}) \ge {\rm Pr}({\rm block\hspace{0.15cm}error}) \hspace{0.05cm}. $$
- A "lower bound" additionally requires knowledge of the weight function $W_i$ for $i = d_{\rm min}$. Thus, the following condition can be satisfied:
- $${\rm Pr}({\rm lower\hspace{0.15cm} bound}) \le {\rm Pr}({\rm block\hspace{0.15cm}error}) \hspace{0.05cm}.$$
Hints:
- The exercise belongs to the chapter "Definition and Properties of Reed-Solomon Codes".
- Reference is made in particular to the page "Singleton Bound and Minimum Distance".
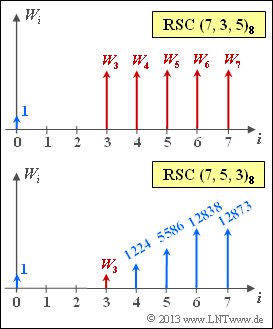
- The weights $W_i$ marked in red in the above graph are to be calculated.
Questions
Solution
- $$W_i = {n \choose i} \cdot \sum_{j = 0}^{i-d}\hspace{0.15cm}(-1)^j \cdot {i \choose j} \cdot \big [\hspace{0.03cm}q^{i\hspace{0.03cm}-\hspace{0.03cm}j\hspace{0.03cm}-\hspace{0.03cm}d\hspace{0.03cm}+\hspace{0.03cm}1}-1 \hspace{0.03cm} \big ]\hspace{0.05cm}.$$
- Because of the minimum distance $d_{\min} = 5$, $W_3 \ \underline{= 0}$ and $W_4 \ \underline{= 0}$. The other weights result in
- $$W_5 = {7 \choose 5} \cdot (8^1 - 1) = \frac {7 \cdot 6 \cdot 5 \cdot4 \cdot 3}{1 \cdot 2 \cdot 3 \cdot4 \cdot 5} \cdot 7 = 21 \cdot 7 \hspace{0.15cm}\underline {= 147}\hspace{0.05cm},$$
- $$W_6 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {7 \choose 6} \cdot \sum_{j = 0}^{1}\hspace{0.15cm}(-1)^j \cdot {6 \choose j} \cdot \big (\hspace{0.03cm}8^{2\hspace{0.03cm}-\hspace{0.03cm}j} -1 \big )=7 \cdot \left [ (8^2 - 1) - 6 \cdot (8^1 - 1)\right ] = 7 \cdot (63-42) \hspace{0.15cm}\underline {= 147}\hspace{0.05cm},$$
- $$W_7 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {7 \choose 7} \cdot \sum_{j = 0}^{2}\hspace{0.15cm}(-1)^j \cdot {7 \choose j} \cdot \big (\hspace{0.03cm}8^{3\hspace{0.03cm}-\hspace{0.03cm}j} -1 \big )= (8^3 - 1) - 7 \cdot (8^2 - 1) +21 \cdot (8^1 - 1) = 511 - 7 \cdot 63 + 21 \cdot 7 \hspace{0.15cm}\underline {= 217}\hspace{0.05cm},$$
- $$\Rightarrow \hspace{0.3cm}W_0 + W_5 + W_6 + W_7 = 1 + 147 + 147 + 217 = 512 = 8^3 = q^k\hspace{0.05cm}.$$
(2) Analogous to subtask (1), we obtain:
- $$W_3 = {7 \choose 3} \cdot (8^1 - 1) = \frac {7 \cdot 6 \cdot 5 }{1 \cdot 2 \cdot 3 } \cdot 7 = 35 \cdot 7 \hspace{0.15cm}\underline {= 245}\hspace{0.05cm}.$$
(3) The falsification probability of a symbol is given by $\varepsilon_{\rm S} = 0.1$.
- Then, for the probability that in a code word with $n = 7$ symbols
- exactly three symbols are falsified:
- $$p_3 = 0.1^3 \cdot 0.9^4 = 0.6561 \cdot 10^{-3} \hspace{0.05cm},$$
- exactly four symbols are falsified:
- $$p_4 = 0.1^4 \cdot 0.9^3 = 0.729 \cdot 10^{-4} \hspace{0.05cm},$$
- exactly five symbols are falsified:
- $$p_5 = 0.1^5 \cdot 0.9^2 = 0.81 \cdot 10^{-5} \hspace{0.05cm},$$
- exactly six symbols are falsified:
- $$p_6 = 0.1^6 \cdot 0.9 = 0.9 \cdot 10^{-6}\hspace{0.05cm},$$
- all $n = 7$ symbols are falsified:
- $$p_7 = 0.1^7 = 10^{-7}\hspace{0.05cm}.$$
⇒ At the $\rm RSC \, (7, \, 3, \, 5)_8$ the zero word can be falsified by symbol errors into one of $q^k - 1 = 8^3 - 1 = 511$ other code words. Thus, using the weight enumerating functions of subtask (1), we obtain:
- $${\rm Pr}({\rm block\hspace{0.15cm}error}) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \frac {W_5 \cdot p_5 + W_6 \cdot p_6 + W_7 \cdot p_7}{511} =\frac {147 \cdot 0.81 \cdot 10^{-5} + 147 \cdot 0.9 \cdot 10^{-6} + 217 \cdot 10^{-7}}{511} \hspace{0.15cm}\underline {\approx 0.263 \cdot 10^{-5}} \hspace{0.05cm}.$$
⇒ At the $\rm RSC \, (7, \, 5, \, 3)_8$ we have to average over $8^5 - 1 = 32767$ falsification probabilities because of $k = 5$. With $W_3 = 245$ from subtask (2) and the weights
- $$W_4 = 1224, \ W_5 = 5586, \ W_6 = 12838, \ W_7 = 12873$$
according to the specification sheet, we obtain for this:
- $${\rm Pr}({\rm block\hspace{0.15cm}error}) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \frac {W_3 \cdot p_3 + W_4 \cdot p_4 + W_5 \cdot p_5 + W_6 \cdot p_6 + W_7 \cdot p_7}{32767} =\frac {245 \cdot 0.656 \cdot 10^{-3} + \hspace{0.15cm}... \hspace{0.15cm}+ 12873 \cdot 10^{-7}}{32767} \hspace{0.15cm}\underline {\approx 0.942 \cdot 10^{-5}} \hspace{0.05cm}. $$
(4) Let only $d_{\rm min}$ $($further abbreviated as $d)$ be known and thus also $p_d = \varepsilon_{\rm S}^d \cdot (1 - \varepsilon_{\rm S})^{n-d}$.
- This is also the upper bound we are looking for:
- ${\rm RSC} \, (7, \, 3, \, 5)_8 \text{:} \hspace{0.33cm} {\rm Pr(upper \ bound)} = p_5 = \underline{0.81 \cdot 10^{-5}}$,
- ${\rm RSC} \, (7, \, 5, \, 3)_8 \text{:} \hspace{0.33cm} {\rm Pr(upper \ bound)} = p_3 = \underline{65.6 \cdot 10^{-5}}$.
- Since the weight $W_d$ was assumed to be unknown, it is set to the maximum possible value $(W_5 = 511$ or $W_3 = 32767)$ so that the prefactors in the equations for subtask (3) disappear. This is the only way to ensure an upper bound.
- In both cases, the upper bound is significantly higher than the results of subtask (3):
- $\rm RSC \, (7, \, 3, \, 5)_8 \text{:} \hspace{0.33cm} 0.810 \cdot 10^{-5}$ instead of $0.263 \cdot 10^{-5}$ $($faktor approx. $3)$,
- $\rm RSC \, (7, \, 5, \, 3)_8 \text{:} \hspace{0.33cm} 65.6 \cdot 10^{-5}$ instead of $0.942 \cdot 10^{-5}$ $($faktor approx. $70)$.
(5) Using the abbreviation $d = d_{\rm min}$, one obtains for the lower bound:
- $${\rm Pr}({\rm lower\hspace{0.15cm} bound})= \frac{W_d \cdot p_d}{q^k -1} \hspace{0.05cm}. $$
- For the $\rm RSC \, (7, \, 3, \, 5)_8$, because of $W_d = W_5$ and $p_d = p_5$, the lower bound is about $11\%$ below the actual value $(0.263 \cdot 10^{-5})$:
- $${\rm Pr}({\rm lower\hspace{0.15cm} bound}) = \frac{147 \cdot 0.81 \cdot 10^{-5}}{511} \hspace{0.15cm}\underline {\approx 0.233 \cdot 10^{-5}}$$
- For the $\rm RSC \, (7, \, 5, \, 3)_8$ holds with $W_d = W_3$ and $p_d = p_3$, the lower bound here deviates from the actual value $(0.942 \cdot 10^{-5})$ more strongly, because in this code the contributions of the higher weights $(W_4, \ W_5, \ W_6, \ W_7)$ are more relevant in relation to $W_3$:
- $${\rm Pr}({\rm lower\hspace{0.15cm} bound}) = \frac{245 \cdot 0.656 \cdot 10^{-3}}{32767} \hspace{0.15cm}\underline {\approx 0.494 \cdot 10^{-5}}\hspace{0.05cm}.$$