Exercise 2.1Z: 2D-Frequency and 2D-Time Representations
From LNTwww
To describe a time-variant channel with several paths, the two-dimensional impulse response is used:
- $$h(\tau,\hspace{0.05cm}t) = \sum_{m = 1}^{M} z_m(t) \cdot {\rm \delta} (\tau - \tau_m)\hspace{0.05cm}.$$
The first parameter $(\tau)$ indicates the delay, the second parameter $(t)$ is related to the time variance of the channel.
The Fourier transform of $h(\tau, \ t)$ with respect to $\tau$ is the time-variant transfer function:
- $$H(f,\hspace{0.05cm} t) \hspace{0.2cm} \stackrel {f,\hspace{0.05cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} h(\tau,\hspace{0.05cm}t) \hspace{0.05cm}.$$
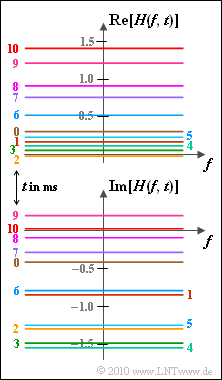
- In the graph, $H(f, \ t)$ is displayed as a function of frequency, for different values of absolute time $t$ in the range of $0 \ \text{...} \ 10 \ \rm ms$.
- In general, $H(f, \ t)$ is complex. The real part (top) and the imaginary part (bottom) are drawn separately.
Notes:
- This task belongs to the chapter General description of time–variant systems.
- In the above equation, an single-path channel is represented with parameter $M = 1$ .
- Here are some numerical values of the specified time-variant transfer function:
- $$H(f,\hspace{0.05cm} t \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0\, {\rm ms}) \approx 0.3 - {\rm j} \cdot 0.4 \hspace{0.05cm},\hspace{0.2cm} H(f,\hspace{0.05cm} t = 2\, {\rm ms}) \approx 0.0 - {\rm j} \cdot 1.3 \hspace{0.05cm},$$
- $$H(f,\hspace{0.05cm} t \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 4\, {\rm ms}) \approx 0.1 - {\rm j} \cdot 1.5 \hspace{0.05cm},\hspace{0.2cm} H(f,\hspace{0.05cm} t = 6\, {\rm ms}) \approx 0.5 - {\rm j} \cdot 0.8 \hspace{0.05cm},$$
- $$H(f,\hspace{0.05cm} t \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 8\, {\rm ms}) \approx 0.9 - {\rm j} \cdot 0.1 \hspace{0.05cm},\hspace{0.2cm} H(f,\hspace{0.05cm} t = 10\, {\rm ms}) \approx 1.4 \hspace{0.05cm}.$$
- As can already be guessed from the above graph, neither the real nor the imaginary part of the 2D transfer function $H(f, \ t)$ are zero-mean.
Questionnaire
Solution
(1) As can be seen in the graph, the transfer function $H(f, \ t)$ depends on $t$. Thus $h(\tau, \ t)$ is also time-dependent. Correct is therefore YES.
(2) If we look at a fixed point in time, for example $t = 2 \ \rm ms$, we obtain the following for the time-variant transfer function:
- $$H(f,\hspace{0.05cm} t = 2\, {\rm ms}) = - {\rm j} \cdot 1.3 \hspace{0.05cm} = {\rm const.}$$
- Thus the corresponding 2D–impulse response is
- $$h(\tau,\hspace{0.05cm} t = 2\, {\rm ms}) = - {\rm j} \cdot 1.3 \cdot \delta (\tau) \hspace{0.05cm} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} M = 1 \hspace{0.05cm}.$$
- There is only one path $(M=1)$. This means that the correct solution is NO.
(3) The correct solution is solution 3:
- There is time variance but no frequency selectivity.
- Options 1 and 2, on the other hand, describe time-invariant systems.
(4) Solution 4 is correct:
- For the AWGN channel, no transfer function can be specified.
- For a two-way channel, $H(f, \ t)$ is not a constant in $f$ for any $t$.
- Since in the $H(f, \ t)$ graph the real and imaginary part have a non-zero mean ⇒ the Rayleigh–channel can also be excluded.
- The data for the present task comes from a Rice channel with following parameters:
- $$\sigma = {1}/{\sqrt{2}} \hspace{0.05cm},\hspace{0.2cm} x_0 = {1}/{\sqrt{2}} \hspace{0.05cm},\hspace{0.2cm}y_0 = -{1}/{\sqrt{2}} \hspace{0.05cm},\hspace{0.2cm} f_{\rm D,\hspace{0.05cm} max} = 100\,\,{\rm Hz}\hspace{0.05cm}.$$