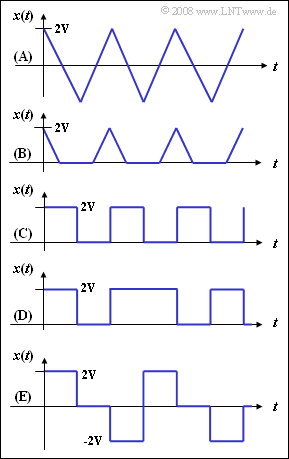
Exercise 2.1Z: Different Signal Courses
On the right are shown five signals. The first three signals $\rm (A)$, $\rm (B)$ and $\rm (C)$ are periodic and thus also deterministic, the two lower signals have stochastic character. The current value of these signals $x(t)$ is taken as a random variable in each case.
Shown in detail are:
$\rm (A)$: A triangular-shaped periodic signal,
$\rm (B)$: the signal $\rm (A)$ after one-way rectification,
$\rm (C)$: a rectangular periodic signal,
$\rm (D)$: a rectangular random signal,
$\rm (E)$: the random signal $\rm (D)$ according to AMI coding;
here the "zero" is preserved, while each "one" is alternately encoded with $+2\hspace{0.03cm}\rm V$ and $-2\hspace{0.03cm} \rm V$.
Hints:
- The exercise belongs to the chapter From Random Experiment to Random Variable.
Questions
Solution
- The random variables $\rm (C)$ and $\rm (D)$ are binary $(M= 2)$,
- while the random variable $\rm (E)$ is trivalent $(M= 3)$.
(2) The proposed solution 1 alone is correct:
- The random variable $\rm (A)$ is continuous in value and can take all values between $\pm 2 \hspace{0.03cm} \rm V$ with equal probability.
- All other random variables are discrete in value.
(3) The proposed solution 2 alone is correct:
- Only the random variable $\rm (B)$ has a discrete part at $0\hspace{0.03cm}\rm V$, and
- also has a continuous component (between $0\hspace{0.03cm} \rm V$ and $+2\hspace{0.03cm}\rm V)$.
(4) According to Bernoulli's law of large numbers:
- $$\rm Pr\left(|\it h_{\rm 0} - \it p_{\rm 0}|\ge\it\varepsilon\right)\le\frac{\rm 1}{\rm 4\cdot \it N\cdot\it\varepsilon^{\rm 2}} = {\it p}_{\rm \hspace{0.01cm}Bernouilli}.$$
- Thus, the probability that the relative frequency $h_0$ deviates from the probability $p_0 = 0.5$ by more than $0.01$ can be calculated as $\varepsilon = 0.01$:
- $${\it p}_{\rm \hspace{0.01cm}Bernoulli} = \rm\frac{1}{4\cdot 100000\cdot 0.01^2}=\rm 2.5\% \hspace{0.5cm}\Rightarrow \hspace{0.5cm} {\rm Min}\big[({\rm Pr}(0.49 \le h_0 \le 0.51)\big] \hspace{0.15cm}\underline{= 97.5\%}.$$
(5) With $p_{\rm Bernoulli} = 1 - 0.99 = 0.01$ and $\varepsilon = 0.001$ holds again by the law of large numbers:
- $${\it p}_{\rm \hspace{0.01cm}Bernoulli}\le\frac{\rm 1}{\rm 4\cdot \it N\cdot\it \varepsilon^{\rm 2}}.$$
- Solved for $N$, one gets:
- $$N\ge\frac{\rm 1}{\rm 4\cdot\it p_{\rm \hspace{0.01cm}Bernoulli}\cdot\varepsilon^{\rm 2}}=\rm \frac{1}{4\cdot 0.01\cdot 0.001^{2}}=\rm 0.25\cdot 10^8 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} {\it N}_{\rm min} \hspace{0.15cm}\underline{= 2.5\cdot 10^9}.$$