Exercise 2.4: GF(2 to the Power of 2) Representation Forms

Three representation forms for ${\rm GF}(2^2)$

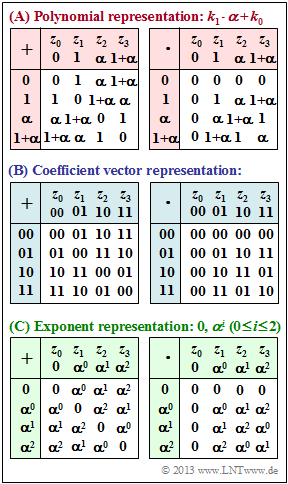
Opposite you can see the addition table as well as the multiplication table for the extension field $\rm GF(2^2)$ in three different variants:

the polynomial representation,

the coefficient vector representation,

the exponent representation.

Hints:

The exercise refers to the chapter "Extension fields".

All necessary information about ${\rm GF}(2^2)$ can be found on the "first page" of this chapter.

In subtask (4) the following expressions are considered:

$$A = z_2 \cdot z_2 + z_2 \cdot z_3 + z_3 \cdot z_3,$$

$$B = (z_0 + z_1 + z_2) \cdot (z_0 + z_1 + z_3).$$

Questions

Solution

(1) The proposed solutions 1, 2 and 5 are applicable. Justification:

If $\alpha = 0$ or $\alpha = 1$, the pseudo element $\alpha$ would be indistinguishable from the other two ${\rm GF}(2)$ elements $0$ and $1$.

The modulo-2 calculation can be recognized from the addition table. For example, $1 + 1 = 0, \ \alpha + \alpha = 0, \ (1 + \alpha) + (1 + \alpha) = 0$, etc.
From the multiplication table we see that $\alpha^2 = \alpha \cdot \alpha = 1 + \alpha$ holds $($3rd row, 3rd column$)$. Thus also

$$\alpha^2 + \alpha + 1 = 0.$$

(2) Correct is the solution suggestion 2. Thus

"$01$" for the element "$1$" and

"$10$" for the element "$\alpha$".

(3) Correct are the solutions 2 and 3:

It is true that $\alpha^0 = 1$ and $\alpha^1 = \alpha$.

For the underlying polynomial $p(x) = x^2 + x + 1$, it follows further from $p(\alpha) = 0$:

$$\alpha^2 +\alpha + 1 = 0 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} \alpha^2 =\alpha + 1 \hspace{0.05cm}.$$

(4) According to the tables of polynomial representation holds:

$$A \hspace{-0.15cm} \ = \ \hspace{-0.15cm} z_2 \cdot z_2 + z_2 \cdot z_3 + z_3 \cdot z_3 = \alpha \cdot \alpha + \alpha \cdot (1+\alpha) + (1+\alpha) \cdot (1+\alpha) = (1+\alpha) + (1) + (\alpha) = 0 = z_0 \hspace{0.05cm},$$

$$ B \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (z_0 + z_1 + z_2) \cdot (z_0 + z_1 + z_3) = (0 + 1 + \alpha) \cdot (0 + 1 + 1+ \alpha) = (1+\alpha) \cdot \alpha = 1 = z_1 \hspace{0.05cm}.$$

Therefore, the proposed solutions 1 and 2 are correct.

The same results are obtained with the coefficient vector representation:

$$A \hspace{-0.15cm} \ = \ \hspace{-0.15cm} z_2 \cdot z_2 + z_2 \cdot z_3 + z_3 \cdot z_3 = (10) \cdot (10) + (10) \cdot (11) + (11) \cdot (11) = (11) + (01) + (10) = (00) = 0 = z_0 \hspace{0.05cm},$$

$$B \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (z_0 + z_1 + z_2) \cdot (z_0 + z_1 + z_3) = [(00) + (01) + (10)] \cdot [(00) + (01) + (11)] =(11) \cdot (10) = (01) = z_1 \hspace{0.05cm}.$$

And finally with the exponent representation:

$$A \hspace{-0.15cm} \ = \ \hspace{-0.15cm} z_2 \cdot z_2 + z_2 \cdot z_3 + z_3 \cdot z_3 = \alpha^1 \cdot \alpha^1 + \alpha^1 \cdot \alpha^2 + \alpha^2 \cdot \alpha^2 = \alpha^2 + \alpha^3 + \alpha^4 = \alpha^2 + \alpha^0 + \alpha^1 = 0 = z_0 \hspace{0.05cm},$$

$$B \hspace{-0.15cm} \ = \ \hspace{-0.15cm}(z_0 + z_1 + z_2) \cdot (z_0 + z_1 + z_3) = [0 + \alpha^0 + \alpha^1] \cdot [0 + \alpha^0 + \alpha^2] = \alpha^2 \cdot \alpha^1 = \alpha^3 = \alpha^0 = z_1 \hspace{0.05cm}.$$

	The elements "$\alpha$" and "$1 + \alpha$" are neither $0$ nor $1$.
	The arithmetic operations are performed modulo $2$.
	The arithmetic operations are performed modulo $4$.
	One recognizes the result $\alpha^2 + \alpha + 1 = 0$ from the addition table.
	One recognizes the result $\alpha^2 + \alpha + 1 = 0$ from the multiplication table.

	No connections can be seen.
	The elements "$0, \ 1$" and "$\alpha$" are the same in both representations.
	The element "$1 + \alpha$" is "$\alpha^2$" in the exponent representation.
	The element "$\alpha^2$" of the exponent representation stands for "$\alpha \cdot (1 + \alpha)$".

	It holds $A = z_0$,
	It holds $A = z_2$,
	It holds $B = z_1$,
	It holds $B = z_3$.

	"$(k_0 \ k_1)"$ refers to the element "$k_1 \cdot \alpha + k_0$".
	"$(k_1 \ k_0)$" refers to the element "$k_1 \cdot \alpha + k_0$".
	There is no relationship between the two representations.