Exercise 2.4Z: Triangular Function
From LNTwww
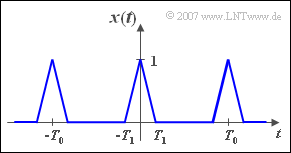
We consider the signal ${x(t)}$ with $T_0$ according to the adjacent sketch, where the second signal parameter $T_1 ≤ T_0/2$ is to apply. This signal is dimensionless and limited to $1$ .
In subtask (3) the Fourier series representation $x_3(t)$ based on only $N = 3$ coefficients is used.
The difference between the truncated Fourier series and the actual signal is:
- $$\varepsilon_3(t)=x_3(t)-x(t).$$
Hints:
- This exercise belongs to the chapter Fourier Series.
- You can find a compact summary of the topic in the two (German language) learning videos
- Zur Berechnung der Fourierkoeffizienten ⇒ "To calculate the Fourier coefficients"
- Eigenschaften der Fourierreihendarstellung ⇒ "Properties of the Fourier series representation"
- To solve the problem, you can use the following definite integral (let $n$ be an integer$)$:
- $$\int u \cdot \cos(au)\,{\rm d}u = \frac{\cos(au)}{a^2} + \frac{u \cdot \sin(au)}{a}.$$
Questions
Solution
(1) Proposed solutions 1 and 2 are correct:
- The DC coefficient is actually $T_1/T_0$. Since ${x(t)}$ is an even function, all sine coefficients $B_n = 0$.
- The even cosine coefficients $A_{2n}$ only disappear if $T_1 = T_0/2$.
- In this case the condition ${x(t)} = 2A_0 - x(t - T_0/2)$ is fulfilled $($with $A_0 = 0.5)$.
(2) Taking advantage of the symmetry property ${x(-t)} = {x(t)}$ one obtains:
- $$A_n=2 \cdot \frac{2}{T_0}\cdot \hspace{-0.1cm}\int_0^{T_1}(1-\frac{t}{T_1})\cos(2\pi n\frac{t}{T_0})\, {\rm d}t.$$
- This leads to two partial integrals $I_1$ and $I_2$. The first is:
- $$I_1=\frac{4}{T_0} \cdot \hspace{-0.1cm} \int_0^{T_1}\cos(2\pi n\frac{t}{T_0})\,{\rm d}t=\frac{2}{\pi n}\sin(2\pi n\frac{T_1}{T_0}).$$
- For the second integral, with the integral on the statement side:
- $$I_2=\frac{-4}{T_0\cdot T_1}\cdot \hspace{-0.1cm}\int_0^{T_1}t\cdot\cos(2\pi n\frac{t}{T_0})\,{\rm d}t=\frac{-4}{T_0\cdot T_1}\cdot \hspace{0.1cm}\left[\frac{T^2_0 \cdot \cos(2\pi nt/T_0)}{4\pi^2n^2}+\frac{T_0 \cdot t \cdot \sin(2\pi nt/T_0)}{2\pi n}\right]^{T_1}_0.$$
- This last integral can be summarised as follows:
- $$I_2=\frac{-\cos(2\pi nT_1/T_0)}{\pi^2 n^2T_1/T_0}+\frac{1}{\pi^2 n^2 T_1/T_0}-I_1.$$
- From this follows with $1 - \cos(2\alpha) = 2 \cdot \sin^2(\alpha)$:
- $$A_n=I_1+I_2=\frac{1-\cos(2\pi nT_1/T_0)}{\pi^2 n^2 T_1/T_0}=\frac{2\sin^2 (\pi nT_1/T_0)}{\pi^2 n^2 T_1/T_0}.$$
- For $T_1/T_0 = 0.25$ one obtains:
- $$A_n=\frac{8\sin^2 (\pi n/4)}{\pi^2 n^2}.$$
- In particular:
- $$A_1=\frac{8}{\pi^2}\sin^2(\pi/4)=\frac{4}{\pi^2}\hspace{0.15cm}\underline{\approx 0.405},\hspace{0.5cm} A_2=\frac{2}{\pi^2}\sin^2(\pi/2)=\frac{2}{\pi^2}\hspace{0.15cm}\underline{\approx 0.202},\hspace{0.5cm} A_3=\frac{8}{9\pi^2}\sin^2(3\pi/4)=\frac{4}{9\pi^2}\hspace{0.15cm}\underline{\approx 0.045}.$$
(3) It holds:
- $$x_3(t)=\frac{1}{4}+\frac{4}{\pi^2}\left[\cos(\omega_0 t)+\frac{1}{2}\cos(2\omega_0 t)+\frac{1}{9}\cos(3\omega_0 t)\right].$$
- At time $t = 0$ this gives:
- $$x_3(t=0)=\frac{1}{4}+\frac{4}{\pi^2}\cdot \frac{29}{18}\approx 0.9 \hspace{0.5cm}\Rightarrow \hspace{0.5cm}\varepsilon_3(t=0)=x_3(t=0)-x(t=0)\hspace{0.15cm}\underline{=-0.1}.$$
- For the time $t = 0$ and for multiples of the period $T_0$ $($peak of the triangular functions in each case$)$ the deviation is greatest in terms of magnitude.