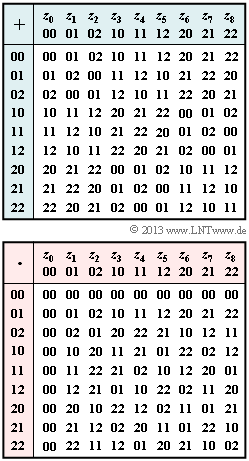
Exercise 2.6: GF(P power m). Which P, which m?

• Return to book

Underlying tables for
addition and multiplication

A Galois field  ${\rm GF}(q)$  with  $q = P^m$  elements defined by the adjacent tables is to be analyzed

• for addition  $($marked with "$+$"$)$,  and

• for multiplication  $($marked with "$\hspace{0.05cm}\cdot\hspace{0.05cm}$)".

This Galois field   ${\rm GF}(q) = \{\hspace{0.1cm}z_0,\hspace{0.1cm} z_1,\hspace{0.05cm} \text{...} , \hspace{0.1cm}z_{q-1}\}$   satisfies all the requirements for a finite field listed in the chapter  "Some Basics of Algebra" . Thus,  commutative, associative and distributive laws are also satisfied.

Furthermore there is

• a neutral element with respect to addition   ⇒   $N_{\rm A}$:

$$\exists \hspace{0.15cm} z_j \in {\rm GF}(q)\text{:} \hspace{0.25cm}z_i + z_j = z_i \hspace{0.3cm} \Rightarrow \hspace{0.3cm} z_j = N_{\rm A} \hspace{0.25cm}{\rm (zero\hspace{0.15cm}element)} \hspace{0.05cm},$$

• a neutral element with respect to multiplication   ⇒   $N_{\rm M}$:

$$\exists \hspace{0.15cm} z_j \in {\rm GF}(q)\text{:} \hspace{0.25cm}z_i \cdot z_j = z_i \hspace{0.3cm} \Rightarrow \hspace{0.3cm} z_j = N_{\rm M} \hspace{0.25cm}{\rm (identity\hspace{0.15cm}element)} \hspace{0.05cm},$$

• for all elements  $z_i$  an additive inverse   ⇒   ${\rm Inv_A}(z_i)$:

$$\forall \hspace{0.15cm} z_i \in {\rm GF}(q)\hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_A}(z_i) \in {\rm GF}(q)\text{:}$$

$$z_i + {\rm Inv_A}(z_i) = N_{\rm A} = {\rm "\hspace{-0.15cm}0\hspace{-0.1cm}"}\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm short}\text{:}\hspace{0.15cm} {\rm Inv_A}(z_i) = - z_i \hspace{0.05cm},$$

• for all elements  $z_i$  except the zero element a multiplicative inverse  ⇒  ${\rm Inv_M}(z_i)$:

$$\forall \hspace{0.15cm} z_i \in {\rm GF}(q),\hspace{0.15cm} z_i \ne N_{\rm A} \hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_M}(z_i) \in {\rm GF}(q)\text{:}$$

$$z_i \cdot {\rm Inv_M}(z_i) = N_{\rm M} = {\rm "\hspace{-0.15cm}1\hspace{-0.1cm}"} \hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm short}\text{:}\hspace{0.15cm} {\rm Inv_M}(z_i) = z_i^{-1} \hspace{0.05cm}.$$

Hints:

• This exercise belongs to the chapter  "Extension Field".

• In the tables,  the elements   $z_0, \hspace{0.05cm} \text{...} \hspace{0.1cm} , \ z_8$   are called  "coefficient vectors".

• For example,  "$2 \hspace{0.03cm}1$"  stands for  "$2 \cdot \alpha + 1$".

Questions

1

Specify the parameters of the Galois field considered here.

$P \ = \ $

$m \ = \ $

$q \ = \ $

2

What is the neutral element of addition?

	The neutral element of addition is  $N_{\rm A} = \,$ "$0\hspace{0.03cm}0$",
	The neutral element of addition is  $N_{\rm A} = \,$ "$0\hspace{0.03cm}1$".

3

What is the neutral element of multiplication?

	The neutral element of multiplication is  $N_{\rm M} = \,$ "$0\hspace{0.03cm}0$",
	The neutral element of multiplication is  $N_{\rm M} = \,$ "$0\hspace{0.03cm}1$".

4

What statements are true regarding additive inverses?

	It holds  ${\rm Inv_A} ($"$0\hspace{0.03cm}2$") $\, = \,$ "$0\hspace{0.03cm}1$",
	It holds  ${\rm Inv_A} ($"$1\hspace{0.03cm}1$") $\, = \,$ "$2\hspace{0.03cm}2$",
	It holds  ${\rm Inv_A} ($"$2\hspace{0.03cm}2$") $\, = \,$ "$0\hspace{0.03cm}0$".

5

Which of the following statements are true about the multiplication?

	The multiplication is defined here modulo  $p(\alpha) = \alpha^2 + 2$.
	The multiplication is defined here modulo  $p(\alpha) = \alpha^2 + 2\alpha + 2$.

6

What statements are true regarding multiplicative inverses?

	There is a multiplicative inverse for all elements  $z_i ∈ {\rm GF}(P^m)$  .
	It holds  ${\rm Inv_M} ($"$1\hspace{0.03cm}2$") $\, = \,$"$1\hspace{0.03cm}0$".
	It holds  ${\rm Inv_M} ($"$2\hspace{0.03cm}1$") $\, = \,$ "$1\hspace{0.03cm}2$".

7

Does  $($"$2\hspace{0.03cm}0$" $\, + \,$ "$1\hspace{0.03cm}2$"$)$ $\, \cdot\,$ "$1\hspace{0.03cm}2$" $\, = \,$"$2\hspace{0.03cm}0$" $\, \cdot\,$ "$1\hspace{0.03cm}2$" $\, + \,$"$1\hspace{0.03cm}2$" $\, \cdot\,$ "$1\hspace{0.03cm}2$" hold?

	Yes.
	No.

Solution

Solution

(1)  Each element consists of two ternaries   ⇒   $\underline{P = 3}, \ \underline{m = 2}$.  There are  $q = P^m = 3^8 = \underline{9 \rm \hspace{0.2cm}elements}$.

(2)  Correct is the  proposed solution 1:

• The neutral element of the addition   $(N_{\rm A})$  satisfies for all  $z_i ∈ {\rm GF}(P^m)$  the condition  $z_i + N_{\rm A} = z_i$.
• From the addition table it can be read that  "$0\hspace{0.03cm}0$"  satisfies this condition.

(3)  Correct is the  proposed solution 2:

• The neutral element of the multiplication   $(N_{\rm M})$  must always satisfy the condition  $z_i \cdot N_{\rm M} = z_i$.

• From the multiplication table,  $N_{\rm M} = \, "\hspace{-0.15cm}0\hspace{0.03cm}1\hspace{-0.1cm}"$.

• In polynomial notation,  this corresponds to  $k_1 = 0$  and  $k_0 = 1$:

$$k_1 \cdot \alpha + k_0 = 1 \hspace{0.05cm}.$$

(4)  With the polynomial representation,  the following calculations result:

$${\rm Inv_A}("\hspace{-0.05cm}0\hspace{0.03cm}2") \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Inv_A}(2) = (-2) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 3 = 1 \hspace{0.25cm}\Rightarrow \hspace{0.25cm}{\rm vector}\hspace{0.15cm}"\hspace{-0.1cm}0\hspace{0.03cm}1\hspace{-0.1cm}"\hspace{0.05cm},$$

$${\rm Inv_A}("\hspace{-0.05cm}1\hspace{0.03cm}1")\hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Inv_A}(\alpha + 1) = \big[(-\alpha) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 3\big] + \big[(-1) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 3\big] =2\alpha + 2 \hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm vector}\hspace{0.15cm}"\hspace{-0.15cm}\hspace{-0.05cm}2\hspace{0.03cm}2\hspace{-0.1cm}"\hspace{0.05cm},$$

$${\rm Inv_A}("\hspace{-0.05cm}2\hspace{0.03cm}2")\hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Inv_A}(2\alpha + 2) = \big[(-2\alpha) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 3\big] + \big[(-2) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 3\big] =\alpha + 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm vector}\hspace{0.15cm}"\hspace{-0.15cm}\hspace{-0.05cm}1\hspace{0.03cm}1\hspace{-0.1cm}"\hspace{0.05cm}.$$

Consequently,  only the  first two proposed solutions  are correct.

However,  the exercise can also be solved without calculation using the addition table alone:

• For example,  you can find the inverse of  "$2\hspace{0.03cm}2$"  by looking for the column with the entry  "$0\hspace{0.03cm}0$"  in the last row.

• You find the column labeled  "$1\hspace{0.03cm}1$"  and thus  ${\rm Inv_A}("\hspace{-0.15cm}2\hspace{0.03cm}2\hspace{-0.15cm}") = \, "\hspace{-0.15cm}1\hspace{0.03cm}1\hspace{-0.15cm}"$.

(5)  Multiplying  $\alpha$  $($vector "$1\hspace{0.03cm}0$"$)$  by itself gives  $\alpha^2$.

• If the first proposed solution were valid,  the condition  $\alpha^2 + 2 = 0$  and thus  $\alpha^2 = (-2) \, {\rm mod} \, 3 = 1$,  thus yielding the vector  "$0\hspace{0.03cm}1$".

• Assuming the second proposed solution,  it follows from the condition  $\alpha^2 + 2\alpha + 2 = 0$   in polynomial notation:

$$\alpha^2 = \big [(-2\alpha) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 3\big] + \big[(-2) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 3\big ] = \alpha + 1$$

and thus the coefficient vector  "$1\hspace{0.03cm}1$".

• In the multiplication table,  in row 4, column 4,  we find exactly the entry  "$1\hspace{0.03cm}1$"   ⇒   So,  the correct answert is the  proposed solution 2.

(6)  The multiplicative inverse to  "$1\hspace{0.03cm}2$"  can be found in row 6 of the multiplication table as the column with the entry  "$0\hspace{0.03cm}1$"  

• So the  proposed solution 2  is correct in contrast to proposal 3.  Namely,  ${\rm Inv_M}("\hspace{-0.15cm}21\hspace{-0.15cm}") = \, "\hspace{-0.15cm}2\hspace{0.03cm}0\hspace{-0.1cm}"$ holds.

• We check these results considering  $\alpha^2 + 2\alpha + 2 = 0$  by multiplications:

$$"\hspace{-0.15cm}1\hspace{0.03cm}2\hspace{-0.1cm}" \hspace{0.05cm}\cdot \hspace{0.05cm}"\hspace{-0.15cm}1\hspace{0.03cm}0\hspace{-0.1cm}" \hspace{0.15cm} \Rightarrow \hspace{0.15cm} (\alpha + 2) \cdot \alpha = \alpha^2 + 2\alpha = (-2\alpha-2) + 2\alpha = -2 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 3 = 1 \hspace{0.15cm} \Rightarrow \hspace{0.15cm} {\rm vector}\hspace{0.15cm}"\hspace{-0.15cm}0\hspace{0.03cm}1\hspace{-0.15cm}" \hspace{0.15cm} \Rightarrow \hspace{0.15cm}{\rm multiplicative \hspace{0.15cm}inverse}\hspace{0.05cm}.$$

$$"\hspace{-0.15cm}2\hspace{0.03cm}1\hspace{-0.1cm}" \hspace{0.05cm}\cdot \hspace{0.05cm}"\hspace{-0.15cm}1\hspace{0.03cm}2\hspace{-0.1cm}" \hspace{0.15cm} \Rightarrow \hspace{0.15cm} (2\alpha + 1) \cdot (\alpha + 2) = 2 \alpha^2 + \alpha + 4\alpha + 2 = 2 \alpha^2 + 5\alpha + 2 = 2 \cdot (-2\alpha - 2) + 5\alpha + 2 = (\alpha - 2) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 3 = \alpha +1$$

$$\hspace{2.725cm} \Rightarrow \ {\rm vector}\hspace{0.15cm}"\hspace{-0.15cm}1\hspace{0.03cm}1\hspace{-0.15cm}" \hspace{0.15cm} \Rightarrow \hspace{0.15cm}{\rm no\hspace{0.15cm}multiplicative \hspace{0.15cm}inverse}\hspace{0.05cm}.$$

• The solution suggestion 1 is therefore not correct,  because there is no multiplicative inverse for  "$00$".

(7)  The two expressions agree   ⇒   YES, as the following calculations show:

$$("\hspace{-0.15cm}20\hspace{-0.1cm}" + "\hspace{-0.15cm}12\hspace{-0.1cm}") \ \cdot "\hspace{-0.15cm}12\hspace{-0.1cm}" \hspace{-0.15cm} \ = \ \hspace{-0.15cm} "\hspace{-0.15cm}02\hspace{-0.1cm}"\cdot "\hspace{-0.15cm}12\hspace{-0.1cm}" \hspace{-0.15cm} \ = \ \hspace{-0.15cm} "\hspace{-0.15cm}21\hspace{-0.1cm}"\hspace{0.05cm},$$

$$"\hspace{-0.15cm}20\hspace{-0.1cm}" \cdot "\hspace{-0.15cm}12\hspace{-0.1cm}" + "\hspace{-0.15cm}12\hspace{-0.1cm}" \cdot "\hspace{-0.15cm}12\hspace{-0.1cm}" \hspace{-0.15cm} \ = \ \hspace{-0.15cm} "\hspace{-0.15cm}02\hspace{-0.1cm}" + "\hspace{-0.15cm}22\hspace{-0.1cm}" \hspace{-0.15cm} \ = \ \hspace{-0.15cm} "\hspace{-0.15cm}21\hspace{-0.1cm}"\hspace{0.05cm}.$$

This means:   The distributive law has been proved at least on a single example.