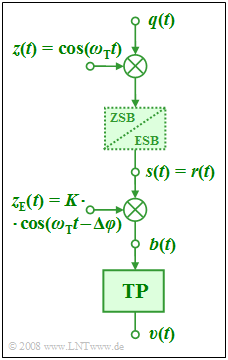
Exercise 2.6Z: Synchronous Demodulator

Amplitude modulator (top),
synchronous demodulator

The depicted block diagram shows a transmission system

with Double-Sideband Amplitude Modulation $\rm(DSB\hspace{0.03cm}–\hspace{-0.1cm}AM)$
and Synchronous Demodulation $\rm (SD)$.

Let the source signal consist of two harmonic oscillations with frequencies $f_2 = 2 \ \rm kHz$ and $f_5 = 5 \ \rm kHz$:

$$q(t) = {2 \, \rm V} \cdot {\rm cos}(\omega_2 t )+ {1 \, \rm V} \cdot {\rm sin}(\omega_5 t ) .$$

This signal is multiplied by the dimensionless carrier signal $z(t) = \cos(\omega_{\rm T} \cdot T)$ of carrier frequency $f_{\rm T} = 50 \ \rm kHz$.
For DSB–AM, the dashed block is irrelevant so that the following holds for the transmission signal:

$$s(t) = q(t) \cdot {\rm cos}(\omega_{\rm T} t ) .$$

In the synchronous demodulator, the received signal $r(t)$ – in an ideal channel identical to the signal $s(t)$ – is multiplied by the receive-site carrier signal $z_{\rm E}(t)$ where the following applies:

$$z_{\rm E}(t) = K \cdot {\rm cos}(\omega_{\rm T} t - \Delta \varphi ) .$$

This signal should not only be frequency-synchronous with $z(t)$ but also phase-synchronous ⇒ hence the name "synchronous demodulator".
The above approach takes into account a phase shift between $z(t)$ and $z_{\rm E}(t)$, which should ideally be $\Delta \varphi = 0$ but often cannot be avoided in real systems.

The output signal $b(t)$ of the second multiplier includes components around twice the carrier frequency in addition to the desired low-frequency component.
Using an ideal low-pass filter $\rm (LP)$ (e.g. with cut-off frequency $f_{\rm T}$) the sink signal $v(t)$, which ideally should be equal to the source signal $q(t)$, can be obtained.

For the transmitter, multiplication by the carrier signal $z(t)$ generally results in two sidebands. In Single-Sideband Modulation (ESB–AM), only one of the two bands is transmitted, for example the lower sideband (USB). Thus, the following is obtained with an ideal channel:

$$r(t) = s(t)= {1 \, \rm V} \cdot {\rm cos}\big [(\omega_{\rm T} - \omega_2 )\cdot t \big ] - {0.5 \, \rm V} \cdot {\rm sin}\big [(\omega_{\rm T} - \omega_5 )\cdot t \big ] .$$

Here, synchronous demodulation results in the following distorted sink signal considering a phase shift $\Delta \varphi$, the constant $K = 4$ and the downstream low-pass filter:

$$v(t)= {1 \, \rm V} \cdot {1}/{2}\cdot 4 \cdot{\rm cos}( \omega_2 t - \Delta \varphi)+ {0.5 \, \rm V} \cdot {1}/{2}\cdot 4 \cdot{\rm sin}( \omega_5 t - \Delta \varphi)$$

$$\Rightarrow \hspace{0.5cm}v(t)= {2 \, \rm V} \cdot{\rm cos}( \omega_2 t - \Delta \varphi)+ {1 \, \rm V} \cdot{\rm sin}( \omega_5 t - \Delta \varphi)$$

In the ideal case of phase-synchronous demodulation $(\Delta \varphi = 0)$, $v(t) = q(t)$ holds again.

Please note:

The exercise belongs to the chapter Linear Distortions.
The topic "amplitude modulation/synchronous demodulator" is discussed in detail in the book Modulation Methods.
The following trigonometric relationships are given:

$$\cos^2(\alpha) = {1}/{2} \cdot \big [ 1 + \cos(2\alpha) \big ] \hspace{0.05cm}, $$

$$\cos(\alpha) \cdot \cos(\beta) = {1}/{2} \cdot \big[ \cos(\alpha - \beta)+ \cos(\alpha + \beta) \big],$$

$$ \sin(\alpha) \cdot \cos(\beta) = {1}/{2} \cdot \big[ \sin(\alpha - \beta)+ \sin(\alpha + \beta) \big] \hspace{0.05cm}.$$

The signal designations result from the German original of this exercise. Here again as a listing $q(t)$ ⇒ source signal, $v(t)$ ⇒ sink signal, $z(t)$ ⇒ transmit-site carrier signal, $s(t)$ ⇒ transmission signal (BP), $r(t)$ ⇒ received signal (BP), $z_{\rm E}(t)$ ⇒ receive-site carrier signal, $b(t)$ ⇒ BP signal before low-pass.

Questions

Solution

(1) The following holds for the band-pass signal after the second multiplier:

$$b(t) = r(t) \cdot z_{\rm E}(t)= q(t) \cdot z(t) \cdot z_{\rm E}(t)= K \cdot q(t)\cdot \cos^2(\omega_{\rm T} t).$$

Using the trigonometric relation $\cos^2(\omega_{\rm T} t) = {1}/{2} \cdot\big[ 1 + \cos(2\omega_{\rm T} t)\big]$, one obtains:

$$b(t) = {K}/{2} \cdot q(t) + {K}/{2} \cdot q(t)\cdot \cos(2\omega_{\rm T} t).$$

The second component is located at around twice the carrier frequency ⇒ $2 f_{\rm T}$.
This is removed by the low-pass filter $($with the cut-off frequency $ f_{\rm G} = f_{\rm T})$ .
Hence, the following is obtained: $v(t) = {K}/{2} \cdot q(t) .$
An ideal demodulation ⇒ $v(t) = q(t)$ is obtained with $\underline {K = 2}$ .

(2) Considering the relation

$$\cos(\omega_{\rm T} t) \cdot \cos(\omega_{\rm T} t - \Delta \varphi) = {1}/{2} \cdot \big[ \cos(\Delta \varphi)+ \cos(2\omega_{\rm T} t - \Delta \varphi) \big]$$

and the downstream low-pass filter, which removes the component at around twice the carrier frequency, the following is obtained here with $ {K = 2}$:

$$v(t) = q(t) \cdot \cos(\Delta \varphi).$$

Proposed solutions 2 and 5 are correct:

A phase shift $\Delta \varphi$ only results in frequency-independent attenuation and not in attenuation distortions or phase distortions.
A phase shift by $\varphi =\pm 60^\circ$ results in halving of the signal amplitude.

(3) Here, proposed solution 4 is correct.

Exactly the same phase shift $\Delta \varphi$ occurs for both summands, and phase distortions occur here:

$$v(t)= {2 \, \rm V} \cdot{\rm cos}\big[ \omega_2 \cdot (t - \tau_2) \big]+ {1 \, \rm V} \cdot{\rm sin}\big[ \omega_5 t \cdot (t - \tau_5)\big],$$

$${\rm where}\hspace{0.5cm}\tau_2 = \frac{\Delta \varphi}{\omega_2} \hspace{0.5cm}\ne \hspace{0.5cm} \tau_5 = \frac{\Delta \varphi}{\omega_5}.$$

A phase shift of $\varphi =60^\circ$ corresponding to $\pi/3$ leads to the following delay times here:

$$\tau_2 = \frac{\pi/3}{2 \pi \cdot 2\,\,{\rm kHz }} \approx 83.3\,{\rm µ s }, \hspace{0.5cm} \tau_5 = \frac{\pi/3}{2 \pi \cdot 5\,\,{\rm kHz }} \approx 33.3\,{\rm µ s }.$$

The lower-frequency signal is thus delayed more.

	$v(t) = q(t)$ holds independently of $\Delta \varphi$ .
	$\Delta \varphi \ne 0$ results in frequency-independent attenuation.
	A phase shift $\Delta \varphi \ne 0$ results in attenuation distortions.
	A phase shift $\Delta \varphi \ne 0$ results in phase distortions.
	$v(t) = q(t)/2$ holds with $\Delta \varphi = \hspace{-0.05cm}-\hspace{0.05cm}60^\circ$.

	Regardless of $\Delta \varphi$, $v(t) = q(t)$ holds.
	$\Delta \varphi \ne 0$ results in frequency-independent attenuation.
	A phase shift $\Delta \varphi \ne 0$ results in attenuation distortions.
	A phase shift $\Delta \varphi \ne 0$ results in phase distortions.
	$v(t) = q(t)/2$ holds with $\Delta \varphi = \hspace{-0.05cm}-\hspace{0.05cm}60^\circ$ .