Exercise 2.7: Coherence Bandwidth
For the delay power-spectral density, we assume an exponential behavior. With ${\it \Phi}_0 = {\it \Phi}_{\rm V}(\tau = 0)$ we have
- $${{\it \phi}_{\rm V}(\tau)}/{{\it \phi}_{\rm 0}} = {\rm e}^{ -\tau / \tau_0 } \hspace{0.05cm}.$$
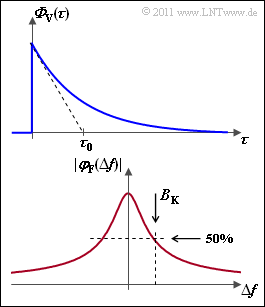
The constant $\tau_0$ can be determined from the tangent in the point $\tau = 0$ according to the upper graph. Note that ${\it \Phi}_{\rm V}(\tau)$ has unit $[1/\rm s]$ . Furthermore,
- The probability density function $\rm (PDF)$ $f_{\rm V}(\tau)$ has the same form as ${\it \Phi}_{\rm V}(\tau)$, but is normalized to area $1$ .
- The average excess delay or mean excess delay $m_{\rm V}$ is equal to the linear expectation $E\big [\tau \big]$ and can be determined from the PDF $f_{\rm V}(\tau)$ .
- The multipath spread or delay spread $\sigma_{\rm V}$ gives the standard deviation of the random variable $\tau$ . In the theory part we also use the term $T_{\rm V}$ for this.
- The displayed frequency correlation function $\varphi_{\rm F}(\Delta f)$ can be calculated as the Fourier transform of the delay power-spectral density ${\it \Phi}_{\rm V}(\tau)$ :
- $$\varphi_{\rm F}(\Delta f) \hspace{0.2cm} {\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} {\it \Phi}_{\rm V}(\tau)\hspace{0.05cm}.$$
- The coherence bandwidth $B_{\rm K}$ is the value of $\Delta f$ at which the frequency correlation function $\varphi_{\rm F}(\Delta f)$ has dropped to half in absolute value.
Notes:
- This exercise belongs to the chapter The GWSSUS Channel Model.
- This exercise requires knowledge of Expected values and moments from the book "Theory of Stochastic Signals".
- In addition, the following Fourier transform is given:
- $$x(t) = \left\{ \begin{array}{c} {\rm e}^{- \lambda \hspace{0.05cm}\cdot \hspace{0.05cm} t}\\ 0 \end{array} \right.\quad \begin{array}{*{1}c} \hspace{-0.35cm} {\rm for} \hspace{0.15cm} t \ge 0 \\ \hspace{-0.35cm} {\rm for} \hspace{0.15cm} t < 0 \\ \end{array} \hspace{0.4cm} {\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet} \hspace{0.4cm} X(f) = \frac{1}{\lambda + {\rm j} \cdot 2\pi f}\hspace{0.05cm}.$$
Questionnaire
Solution
- $$\int_{0}^{+\infty} {\it \Phi}_{\rm V}(\tau) \hspace{0.15cm}{\rm d} \tau = {\it \Phi}_{\rm 0} \cdot \int_{0}^{+\infty} {\rm e}^{-\tau / \tau_0} \hspace{0.15cm}{\rm d} \tau = {\it \Phi}_{\rm 0} \cdot \tau_0 \hspace{0.05cm}. $$
- Then the probability density function is
- $$f_{\rm V}(\tau) = \frac{{\it \Phi}_{\rm V}(\tau) }{{\it \Phi}_{\rm 0} \cdot \tau_0}= \frac{1}{\tau_0} \cdot {\rm e}^{-\tau / \tau_0} \hspace{0.05cm}.$$
- Solution 2 is correct.
(2) The $k$-th moment of an one-sided exponential random variable is $m_k = k! \cdot \tau_0^k$.
- With $k = 1$, this results in the linear mean value $m_1 = m_{\rm V}$:
- $$m_{\rm V} = \tau_0 \hspace{0.1cm} \underline {= 1\,{\rm µ s}} \hspace{0.05cm}. $$
(3) According to the Steiner's Theorem, the variance of any random variable is $\sigma^2 = m_2 \, -m_1^2$.
- This yields $m_2 = 2 \cdot \tau_0^2$, and therefore
- $$\sigma_{\rm V}^2 = m_2 - m_1^2 = 2 \cdot \tau_0^2 - (\tau_0)^2 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \sigma_{\rm V} = \tau_0 \hspace{0.1cm} \underline {= 1\,{\rm µ s}} \hspace{0.05cm}. $$
(4) ${\it \Phi}_{\rm V}(\tau)$ is identical to $x(t)$ in the given Fourier transform pair if $t$ is replaced by $\tau$ and $\lambda$ by $1/\tau_0$.
- Thus, $\varphi_{\rm F}(\Delta f)$ is equal to $X(f)$ with the substitution $f → \Delta f$:
- $$\varphi_{\rm F}(\Delta f) = \frac{1}{1/\tau_0 + {\rm j} \cdot 2\pi \Delta f} = \frac{\tau_0}{1 + {\rm j} \cdot 2\pi \cdot \tau_0 \cdot \Delta f}\hspace{0.05cm}.$$
- The first expression is correct.
(5) The coherence bandwidth is implicit in the following equation:
- $$|\varphi_{\rm F}(\Delta f = B_{\rm K})| \stackrel {!}{=} \frac{1}{2} \cdot |\varphi_{\rm F}(\Delta f = 0)| = \frac{\tau_0}{2}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}|\varphi_{\rm F}(\Delta f = B_{\rm K})|^2 = \frac{\tau_0^2}{1 + (2\pi \cdot \tau_0 \cdot B_{\rm K})^2} \stackrel {!}{=} \frac{\tau_0^2}{4}$$
- $$\Rightarrow \hspace{0.3cm}(2\pi \cdot \tau_0 \cdot B_{\rm K})^2 = 3 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} B_{\rm K}= \frac{\sqrt{3}}{2\pi \cdot \tau_0} \approx \frac{0.276}{ \tau_0}\hspace{0.05cm}. $$
- With $\tau_0 = 1 \ \ \rm µ s$, the coherence bandwidth is $B_{\rm K} \ \underline {= 276 \ \ \rm kHz}$.