Exercise 3.09Z: Viterbi Algorithm again

• Return to book

Trellis for a rate-1/2 code and memory  $m = 1$

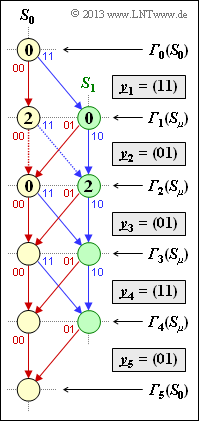
The diagram shows the trellis of the convolutional code according to  $\text{Exercise 3.6}$,  characterized by the following quantities:

• Rate 1/2  ⇒   $k = 1, \ n = 2$,

• memory  $m = 1$,

• transfer function matrix  $\mathbf{G}(D) = (1, \ 1 + D)$,

• length of the information sequence:  $L = 4$,

• sequence length including termination:  $L\hspace{0.05cm}' = L + m = 5$.

On the basis of this representation,  the Viterbi decoding is to be understood step-by-step,  starting from the following received sequence:  

$$\underline{y} = (11, \, 01, \, 01, \, 11, \, 01).$$

Into the trellis are drawn:

• The initial value  ${\it \Gamma}_0(S_0)$  for the Viterbi algorithm,  which is always chosen to  $0$.

• The two error values for the first decoding step  $(i = 1)$  are obtained with  $\underline{y}_1 = (11)$  as follows:

$${\it \Gamma}_1(S_0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\it \Gamma}_0(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} (11) \big ) = 2 \hspace{0.05cm},$$

$${\it \Gamma}_1(S_1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\it \Gamma}_0(S_0) + d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} (11) \big ) = 0 \hspace{0.05cm}.$$

• The error values for step  $i = 2$   ⇒   $\underline{y}_2 = (01)$  are obtained by the following comparisons:

$${\it \Gamma}_2(S_0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [{\it \Gamma}_{1}(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} (01) \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{1}(S_1) + d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) \right ]$$

$$\Rightarrow\hspace{0.3cm} {\it \Gamma}_2(S_0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm min} \big [ 2+1\hspace{0.05cm},\hspace{0.05cm} 0+0 \big ] = 0\hspace{0.05cm},$$

$${\it \Gamma}_2(S_1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [{\it \Gamma}_{1}(S_0) + d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} (01) \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{1}(S_1) + d_{\rm H} \big ((10)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) \right ]$$

$$\Rightarrow\hspace{0.3cm} {\it \Gamma}_2(S_1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm min} \big [ 2+1\hspace{0.05cm},\hspace{0.05cm} 0+2 \big ] = 2\hspace{0.05cm}.$$

In the same way you are

• to compute the error values at time points  $i = 3, \ i = 4$  and  $i = 5$  $($termination$)$,  and

• to eliminate the less favorable paths to a node  ${\it \Gamma}_i(S_{\mu})$  in each case;  in the graph this is indicated by dotted lines for  $i = 2$ .

⇒   Then the continuous path from  ${\it \Gamma}_0(S_0)$  to  ${\it \Gamma}_5(S_0)$  is to be found,  where the backward direction is recommended. 

⇒   If one follows the found path in forward direction,  one recognizes:

• the most likely decoded sequence  $\underline{z}$  $($ideally equal  $\underline{x})$  by the labels,

• the most probable information sequence  $\underline{v}$  $($ideally equal  $\underline{u})$  at the colors.

Hints:  This exercise belongs to the chapter  "Decoding of Convolutional Codes".

Questions

1

Calculate the minimum error values for time  $i = 3$.

${\it \Gamma}_3(S_0) \ = \ $

${\it \Gamma}_3(S_1) \ = \ $

2

Calculate the minimum error values for time  $i = 4$.

${\it \Gamma}_4(S_0) \ = \ $

${\it \Gamma}_4(S_1) \ = \ $

3

Calculate the final error value for time  $i = 5$.

${\it \Gamma}_5(S_0) \ = \ $

4

What are the final results of the Viterbi algorithm:

	$\underline{z} = (11, \, 01, \, 00, \, 11, \, 01)$.
	$\underline{z} = (11, \, 01, \, 11, \, 01, \, 00)$.
	$\underline{v} = (1, \, 0, \, 0, \, 1, \, 0)$.
	$\underline{v} = (1, \, 0, \, 1, \, 0, \, 0)$.

5

What decision would have been made without scheduling?

	The same,
	another.

Solution

Solution

Trellis with branch metrics

Path finding

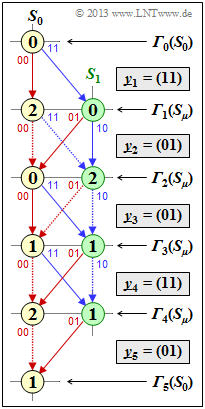
(1)  Starting from  ${\it \Gamma}_2(S_0) = 0, \ \ {\it \Gamma}_2(S_1) = 2$  we get  $\underline{y}_3 = (01)$:

$${\it \Gamma}_3(S_0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm min} \left [0 + d_{\rm H} \big ((00), (01) \big ), \hspace{0.05cm}2 + d_{\rm H} \big ((01), (01) \big ) \right ] = {\rm min} \left [ 0+1\hspace{0.05cm},\hspace{0.05cm} 2+0 \right ] \hspace{0.15cm}\underline{= 1}\hspace{0.05cm},$$

$${\it \Gamma}_3(S_1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [0 + d_{\rm H} \big ((11), (01) \big ), \hspace{0.05cm}2 + d_{\rm H} \big ((10), (01) \big ) \right ] {\rm min} \left [ 0+1\hspace{0.05cm},\hspace{0.05cm} 2+2 \right ] \hspace{0.15cm}\underline{= 1}\hspace{0.05cm}.$$

⇒   Eliminated are the two (dotted)  subpaths that start from state  $S_1$  at time  $i = 2$  $($i.e.,  at the third decoding step$)$.

(2)  Analogous to subtask  (1),  we obtain with  $y_4 = (11)$:

$${\it \Gamma}_4(S_0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [1 + d_{\rm H} \big ((00), (11) \big ), \hspace{0.05cm}1 + d_{\rm H} \big ((01), (11) \big ) \right ] = {\rm min} \left [ 1+2\hspace{0.05cm},\hspace{0.05cm} 1+1 \right ] \hspace{0.15cm}\underline{= 2}\hspace{0.05cm},$$

$${\it \Gamma}_4(S_1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [1 + d_{\rm H} \big ((11), (11) \big ), \hspace{0.05cm}1 + d_{\rm H} \big ((10), (11) \big ) \right ] ={\rm min} \left [ 1+0\hspace{0.05cm},\hspace{0.05cm} 1+1 \right ] \hspace{0.15cm}\underline{= 1}\hspace{0.05cm}$$

⇒   Elimination in the fourth decoding step of the two subpaths  "$S_0 → S_0$"  and  "$S_1 → S_1$".

(3)  For  $i = 5$   ⇒   the  "termination"  is obtained with  $\underline{y}_5 = (01)$:

$${\it \Gamma}_5(S_0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [2 + d_{\rm H} \big ((00), (01) \big ), \hspace{0.05cm}1 + d_{\rm H} \big ((01), (01) \big ) \right ] {\rm min} \left [ 2+1\hspace{0.05cm},\hspace{0.05cm} 1+0 \right ] \hspace{0.15cm}\underline{= 1}\hspace{0.05cm}.$$

⇒   To be eliminated is the subpath  "$S_0 → S_0$".

(4)  The backward search of the continuous path  from ${\it \Gamma}_5(S_0)$  to  ${\it \Gamma}_0(S_0)$  yields

$$S_0 ← S_1 ← S_0 ← S_0 ← S_1 ← S_0.$$

In the forward direction,  this yields the path  "$S_0 → S_1 → S_0 → S_0 → S_1 → S_0$" and thus the

• the most likely code sequence  $\underline{z} = (11, \, 01, \, 00, \, 11, \, 01)$,

• the most likely information  sequence $\underline{v} = (1, \, 0, \, 0, \, 1, \, 0)$.

Thus,  the  proposed solutions 1 and 3  are correct:

• Comparison with the received vector  $\underline{y} = (11, \, 01, \, 01, \, 11, \, 01)$  shows that the sixth bit was falsified during transmission.

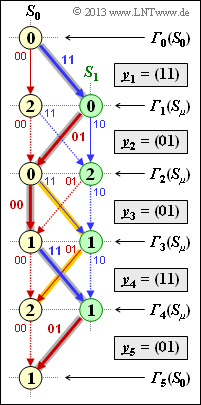
(5)  Without termination ⇒ final decision at  $i = 4$,  there would have been two continuous paths:

• from  "$S_0 → S_1 → S_0 → S_1 → S_0$"  $($shown in yellow$)$,

• from  "$S_0 → S_1 → S_0 → S_0 → S_1$"  $($the ultimately correct path$)$.

The constraint decision at time  $i = 4$  would have led here to the second path and thus to the result  $\underline{v} = (1, \, 0, \, 0, \, 1)$  because of  ${\it \Gamma}_4(S_1) < {\it \Gamma}_4(S_0)$.

• In the considered example,  therefore,  to the  same decision  as in subtask  (4)  with termination bit.

• However,  there are many constellations where only the termination bit enables the correct and safe decision.