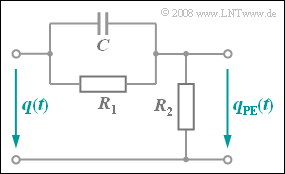
Exercise 3.11: Pre-Emphase and De-Emphase
In voice and audio signal transmission, the signal frequency band is pre-distorted before the FM modulator via an RC high-pass filter according to the diagram. This measure is called "pre-emphasis" $\rm (PE)$.
The amplitude response of the preemphasis network, together with
- the two cutoff frequencies $f_{\rm G1} = (2π · R_1 · C)^{–1}$ and $f_{\rm G2} = f_{\rm G1}/α_0$, as well as
- the DC signal transmission factor $α_0 = R_2/(R_1 + R_2)$
is given by:
- $$ |H_{\rm PE} (f)| = \alpha_0 \cdot \sqrt{\frac{1 + (f/f_{\rm G1})^2}{1 + (f/f_{\rm G2})^2}} \hspace{0.05cm}.$$
For practical purposes, we can assume that the maximum message frequency $f_{\rm N}$ is much smaller than $f_{\rm G2}$ .
If we further consider that the DC signal transmission factor $α_0$ can be changed by an amplification of nbsp;$α$ , we can further assume the following pre-emphasis frequency response where $(f_{\rm G} = f_{\rm G1} = 3 \ \rm kHz)$:
- $$|H_{\rm PE} (f)| \approx \alpha \cdot \sqrt{{1 + \left({f}/{f_{\rm G}}\right)^2}} \hspace{0.05cm}.$$
In this network, the frequency deviation is $Δf_{\rm A}$ as a function of the message frequency $f_{\rm N}$:
- $$ \Delta f_{\rm A} (f_{\rm N}) = \Delta f_{\rm A, \hspace{0.08cm}min} \cdot \sqrt{{1 + \left({f_{\rm N}}/{f_{\rm G}}\right)^2}} \hspace{0.05cm}.$$
- Here $Δf_\text{A, min}$ is the frequency deviation for very small frequencies $(f_{\rm N} → 0)$.
- This parameter should be chosen so that the maximum frequency deviation $Δf_\text{A, max}$ does not exceed $45 \ \rm kHz$.
In order not to distort the useful signal, this pre-emphasis must be rebalanced by a "de-emphasis" network at the receiver. The goal and purpose of preemphasis/deemphasis is solely to reduce the dependence of the signal-to-noise power ratio on the signal frequency.
In this task, the following quantities are used:
- Sink SNR in double-sideband amplitude modulation (DSB-AM) $\rm (DSB–AM)$:
- $$\rho_{{\rm AM} } = \frac{P_{\rm S}}{N_0 \cdot f_{\rm N} } = \xi\hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{{\rm AM} } = 10 \cdot {\rm lg} \hspace{0.15cm}\xi \hspace{0.05cm},$$
- Sink SNR and sink-to-noise ratio in frequency modulation $\rm (FM)$ without pre-emphasis/de-emphasis:
- $$ \rho_{\rm FM} = {3}/{2 } \cdot \eta^2 \cdot \rho_{\rm AM } \hspace{0.3cm}\Rightarrow \hspace{0.3cm} G_{\rm FM} = 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{\rm FM} - 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{\rm AM}= 10 \cdot {\rm lg} \hspace{0.15cm}{3}/{2 } \cdot \eta^2 \hspace{0.05cm},$$
- Sink SNR and sink-to-noise ratio in frequency modulation $\rm (FM)$ using pre-emphasis/de-emphasis:
- $$ \rho_{\rm DE} = \frac{(f_{\rm N}/f_{\rm G})^3}{3 \cdot (f_{\rm N}/f_{\rm G} - \arctan (f_{\rm N}/f_{\rm G}) } \hspace{0.3cm}\Rightarrow \hspace{0.3cm} G_{\rm DE} = 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{\rm DE} - 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{\rm FM}\hspace{0.05cm}$$
Hints:
- This exercise belongs to the chapter Influence of Noise on Systems with Angle Modulation.
- Particular reference is made to the section Pre-emphasis and de-emphasis.
- Throughout the task, assume a message signal containing frequencies up to and including $B_{\rm NF}= 9 \ \rm kHz$ .
Questions
Solution
- The magnitude frequency response of the de-emphasis network is defined as follows:
- $$ |H_{\rm DE} (f)| = \frac{1}{|H_{\rm PE} (f)|}= \frac{1}{\alpha}\cdot \frac{1}{\sqrt{1 + (f/f_{\rm G})^2}} \hspace{0.05cm}.$$
- The frequency response of a simple RC low-pass filter - also known as a first-order low-pass filter - is:
- $$ H_{\rm RC-TP} (f) = \frac{1}{{1 + {\rm j}\cdot f/f_{\rm G}}} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} |H_{\rm RC-TP} (f)| = \frac{1}{\sqrt{1 + (f/f_{\rm G})^2}}\hspace{0.05cm}.$$
(2) The frequency modulation is designed for the maximum frequency $B_{\rm NF} = f_\text{N, max}= 9 \ \rm kHz$ . Then the (maximum) frequency deviation should be $Δf_{\rm A} = 45\ \rm kHz$ .
- From this it follows for the modulation index:
- $$ \eta = \frac{\Delta f_{\rm A}}{f_{\rm N} } = 5 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} G_{\rm FM} (f_{\rm N} = 9\,{\rm kHz}) = 10 \cdot {\rm lg} \hspace{0.15cm}(1.5 \cdot 5^2) \hspace{0.15cm}\underline {\approx 15.74\,{\rm dB}} \hspace{0.05cm}.$$
- Using the message frequency $ f_{\rm N} = 3 \ \rm kHz$ results in a modulation index larger by a factor of $3$ and thus a signal-to-noise ratio larger by a factor of $10 · \lg \ 9 = 9.54 \ \rm dB$ :
- $$G_{\rm FM} (f_{\rm N} = 3\,{\rm kHz}) = 10 \cdot {\rm lg} \hspace{0.15cm}(1.5 \cdot 15^2) \hspace{0.15cm}\underline {\approx 25.28\,{\rm dB}} \hspace{0.05cm}.$$
- Another gain results from the transition from $3\ \rm kHz$ to $1\ \rm kHz$:
- $$G_{\rm FM} (f_{\rm N} = 1\,{\rm kHz}) = 25.28\,{\rm dB} + 9.54\,{\rm dB}\hspace{0.15cm}\underline {= 34.82\,{\rm dB}} \hspace{0.05cm}.$$
(3) The maximum frequency deviation is obtained for $f_{\rm N} = B_{\rm NF}$.
- It follows, with $f_{\rm G} = 3 \ \rm kHz$ and $B_{\rm NF} = 9 \ \rm kHz$:
- $$\Delta f_{\rm A} (B_{\rm NF}) = \Delta f_{\rm A, \hspace{0.08cm}min} \cdot \sqrt{{1 + \left(\frac{B_{\rm NF}}{f_{\rm G}}\right)^2}} = \sqrt {10} \cdot \Delta f_{\rm A, \hspace{0.08cm}min}= \Delta f_{\rm A, \hspace{0.08cm}max} = 45\,{\rm kHz}$$
- $$\Rightarrow \hspace{0.3cm} \Delta f_{\rm A, \hspace{0.08cm}min} = \frac{45\,{\rm kHz}}{\sqrt {10}}\hspace{0.15cm}\underline {\approx 14.23\,{\rm kHz}}\hspace{0.05cm}.$$
(4) Using the given formula, the following "gains due to pre-emphasis/de-emphasis" are obtained:
- $$G_{\rm DE} (f_{\rm N} = 9\,{\rm kHz}) = 10 \cdot {\rm lg}\hspace{0.15cm} \frac{(f_{\rm N}/f_{\rm G})^3}{3 \cdot (f_{\rm N}/f_{\rm G} - \arctan (f_{\rm N}/f_{\rm G}) }= 10 \cdot {\rm lg}\hspace{0.15cm} \frac{3^3}{3 \cdot (3 - 1.249) }\hspace{0.15cm}\underline {\approx 7.1\,{\rm dB}}\hspace{0.05cm},$$
- $$ G_{\rm DE} (f_{\rm N} = 3\,{\rm kHz}) = 10 \cdot {\rm lg}\hspace{0.15cm} \frac{1^3}{3 \cdot (1 - \pi/4) }\hspace{0.15cm}\underline {\approx 1.9\,{\rm dB}}\hspace{0.05cm},$$
- $$G_{\rm DE} (f_{\rm N} = 1\,{\rm kHz}) = 10 \cdot {\rm lg}\hspace{0.15cm} \frac{(1/3)^3}{3 \cdot (1/3 - 0.322) }\hspace{0.15cm}\underline {\approx 0.28\,{\rm dB}}\hspace{0.05cm}.$$