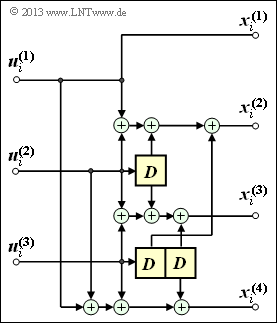
Exercise 3.1: Analysis of a Convolutional Encoder
We consider the outlined convolutional encoder and assume the following information sequence:
- $$\underline{\it u} = \big( 0,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm}\text{...} \big )\hspace{0.05cm}.$$
This sequence is divided into three strands:
- $$\underline{\it u}^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \big( 0,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm} \text{...} \big )\hspace{0.05cm},$$
- $$\underline{\it u}^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \big( 1,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm}\text{...} \big )\hspace{0.05cm},$$
- $$\underline{\it u}^{(3)} \hspace{-0.15cm} \ = \hspace{-0.15cm} \big( 1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm}\text{...} \big )\hspace{0.05cm}.$$
The bits present at the coder at time $i$ are denoted by $u_i^{\rm (1)}$, $u_i^{\rm (2)}$ and $u_i^{\rm (3)}$ . For example $u_1^{\rm (1)} = 0$, $u_2^{\rm (2)} = 1$, $u_3^{\rm (3)} = 1$.
The purpose of this exercise is to determine
- the number $k$ of information bits processed per coding step,
- the number $n$ of code bits output per coding step,
- the memory order (or, for short, the memory) $m$,
- the total influence length (or for short: influence length) $\nu$.
For the given information sequence $\underline {u}$ you shall determine the code symbols $x_i^{(1)}$, $x_i^{(2)}$, $x_i^{(3)}$ and $x_i^{(4)}$ for the clock instants $i = 1$ and $i = 3$. It must be assumed that all memory elements were filled with zeros at the beginning.
Hints:
- This exercise refers to the chapter "Basics of Convolutional Coding".
- For completeness, the code bits to the clock step $i = 2$ are also given here:
- $$x_2^{(1)} = 1 \hspace{0.05cm},\hspace{0.4cm}x_2^{(2)} = 0 \hspace{0.05cm},\hspace{0.4cm} x_2^{(3)} = 0 ,\hspace{0.4cm}x_2^{(4)} = 0 \hspace{0.05cm}.$$
- However, this last specification is not needed to solve the exercise.
Questions
Solution
(2) We denote here the influence lengths of the information sequences $\underline{u}^{(j)}$ by $\nu_j$, where $1 ≤ j ≤ k = 3$ is to be set. Then holds:
- $$\nu_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0 \hspace{0.15cm}{\rm (for \hspace{0.15cm}the \hspace{0.15cm}first \hspace{0.15cm}sequence\hspace{0.15cm}no \hspace{0.15cm}shift \hspace{0.15cm}register \hspace{0.15cm}is \hspace{0.15cm}necessary)}\hspace{0.05cm},\hspace{0.2cm} \nu_2 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1\hspace{0.05cm},\hspace{0.2cm}\nu_3 = 2\hspace{0.05cm}.$$
- The memory order $m$ $($or memory for short$)$ of the encoder is given by the longest shift register ⇒ $\underline {m = 2}$.
- The total influence length $($or influence length for short$)$ is equal to the number of memory elements of the entire encoder circuit ⇒ $\underline {\nu = 3}$.
(3) In general, for the $n = 4$ code bits of step $i$:
- $$x_i^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} \hspace{0.05cm},$$
- $$x_i^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} + u_{i}^{(2)} + u_{i-1}^{(2)} + u_{i-1}^{(3)} \hspace{0.05cm},$$
- $$x_i^{(3)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(2)} + u_{i}^{(3)}+ u_{i-1}^{(2)} + u_{i-2}^{(3)} \hspace{0.05cm},$$
- $$x_i^{(4)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} + u_{i}^{(2)} + u_{i}^{(3)}+ u_{i-2}^{(3)}\hspace{0.05cm}.$$
- In the first coding step, all memory elements are assigned zeros.
- Therefore for $i = 1$ all bits with the indices $i \, –1$ or $i \, –2$ can be omitted.
- In accordance with the specification, let further hold: $u_1^{(1)} = 0$, $u_1^{(2)} = 1$, $u_1^{(3)} = 1$.
- This is obtained by modulo-2 addition:
- $$x_1^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{1}^{(1)} \hspace{0.15cm}\underline {=0} \hspace{0.05cm},$$
- $$x_1^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{1}^{(1)} + u_{1}^{(2)} = 0+1 \hspace{0.15cm}\underline {=1} \hspace{0.05cm},$$
- $$x_1^{(3)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{1}^{(2)} + u_{1}^{(3)}= 1 + 1 \hspace{0.15cm}\underline {=0}\hspace{0.05cm},$$
- $$x_1^{(4)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{1}^{(1)} + u_{1}^{(2)} + u_{1}^{(3)}= 0+1+1\hspace{0.15cm}\underline {=0}\hspace{0.05cm}.$$
(4) In the coding step $i = 3$ the information bits are:
- $$u_i^{(1)} \hspace{-0.2cm} \ = \ \hspace{-0.2cm}1\hspace{0.05cm},\hspace{0.2cm}u_{i-1}^{(1)} = 1\hspace{0.05cm},\hspace{0.2cm}u_{i-2}^{(1)} = 0\hspace{0.05cm},$$
- $$u_i^{(2)} \hspace{-0.2cm} \ = \ \hspace{-0.2cm}0\hspace{0.05cm},\hspace{0.2cm}u_{i-1}^{(2)} = 1\hspace{0.05cm},\hspace{0.2cm}u_{i-2}^{(2)} = 1\hspace{0.05cm},$$
- $$u_i^{(3)} \hspace{-0.2cm} \ = \ \hspace{-0.2cm}1\hspace{0.05cm},\hspace{0.2cm}u_{i-1}^{(3)} = 0\hspace{0.05cm},\hspace{0.2cm}u_{i-2}^{(3)} = 1\hspace{0.05cm},$$
- which results in the following code bits:
- $$x_3^{(1)} \hspace{0.15cm}\underline {=1} \hspace{0.05cm},\hspace{0.4cm}x_3^{(2)} = 1+0+1+0\hspace{0.15cm}\underline {=0}\hspace{0.05cm},\hspace{0.4cm}x_3^{(3)}= 0+1+1+1 \hspace{0.15cm}\underline {=1} \hspace{0.05cm},\hspace{0.4cm}x_3^{(4)} = 1+0+1+1\hspace{0.15cm}\underline {=1}\hspace{0.05cm}.$$
⇒ The code bits in the coding step $i = 2$ have already been mentioned on the information page. Here still follows the derivation:
- $$x_2^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{2}^{(1)} = 1 \hspace{0.05cm},$$
- $$x_2^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{2}^{(1)} + u_{2}^{(2)} + u_{1}^{(2)} + u_{1}^{(3)} = 1+1+1+1 = 0 \hspace{0.05cm},$$
- $$x_2^{(3)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{2}^{(2)} + u_{2}^{(3)}+ u_{1}^{(2)} + u_{0}^{(3)} = 1+0+1+(0) = 0\hspace{0.05cm},$$
- $$x_2^{(4)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{2}^{(1)} + u_{2}^{(2)} + u_{2}^{(3)}+ u_{0}^{(3)}= 1+1+0+(0) = 0\hspace{0.05cm}.$$
- Thus, the code sequence $\underline {x}$ $($after multiplexing$)$ starts with $(0100, 1000, 1011, \ \text{...})$.
- The grouping was done here only for clarity.