Loading [MathJax]/jax/output/HTML-CSS/fonts/TeX/fontdata.js

Exercise 3.5: Recursive Filters for GF(2)

From LNTwww

General recursive filter  (above)
and considered realization  (below)

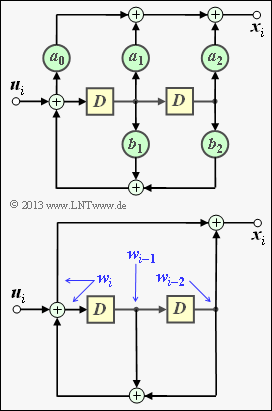
The upper of the two circuits on the right shows a second order recursive filter in general form.  With

A(D) = a0+a1⋅D+a2⋅D2,
B(D) = 1+b1⋅D+b2⋅D2

one obtains for the transfer function

G(D)=A(D)B(D)=a0+a1⋅D+a2⋅D21+b1⋅D+b2⋅D2.
  • It should be noted that all arithmetic operations refer to  GF(2). 
  • Thus,  the filter coefficients   a0, a1, a2, b1, b2   are also binary (0  or  1).


The bottom graph shows the filter specific to the exercise at hand:

  1.   A filter coefficient results in   ai=1   if the connection is through  (0≤i≤2).
  2.   Otherwise,  ai=0.   The same system applies to the coefficients  b1  and  b2.


In the subtasks  (1), ... , (3)  you are to determine the respective output sequence  x_  for different input sequences

  • u_=(1,0,0,0,0,0,0,0,...),
  • u_=(0,1,0,1,0,0,1,1,...),
  • u_=(1,1,1,0,0,0,0,0,...)


using the given circuit.  It should be taken into account:

  • If the input sequence  u_  consists of a  "1"  followed by all zeros,  this specific output sequence  x_  is the  "impulse response"  g_,  and it holds:
g_∘−−D−∙G(D).
  • Otherwise,  the output sequence results as the  "convolution product"  between the input sequence and the impulse response:
x_=u_∗g_.
  • The convolution operation can be bypassed with the  "D-transform" .




Hints:


Questions

1

What statements hold for the impulse response  g_  of the recursive filter?

It holds  g_=(0,1,1,0,1,0,0,1,...).
It holds  g_=(1,1,1,0,1,1,0,1,...).
The impulse response  g_  is infinitely extended.

2

Let now  u_=(0,1,0,1,0,0,1,1).  Which statements are true?

The output sequence is:  x_=(0,1,1,0,1,0,0,1,...).
The output sequence is:  x_=(1,1,1,0,1,1,0,1,...).
The output sequence  x_  extends to infinity.

3

Now apply  u_=(1,1,1).  Which statements are true?

The output sequence  x_  starts with  (1,0,1).
The output sequence  x_  begins with  (1,1,1).
The output sequence  x_  extends to infinity.

4

What statements are valid for the transfer function  G(D)?

It holds  G(D)=(1+D2)/(1+D+D2).
It holds  G(D)=(1+D+D2)/(1+D2).
It holds  G(D)=1+D+D2+D4+D5+D7+D8+... .


Solution

Solution

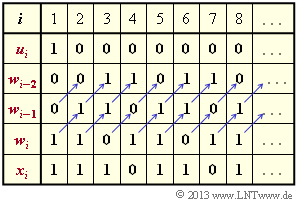
(1)  Correct are the  proposed solutions 2 and 3:

For calculation of the impulse response  g_
For calculation of the output sequence x_
  • The impulse response  g_  is equal to the sequence  x_  for the input sequence  u_=(1,0,0,...). 
  • Based on the filter structure,  w0=w−1=0  and the equations
wi = ui+wi−1+wi−2,
xi = wi+wi−2
the result is  g_=x_=(1,1,1,0,1,1,0,1,...)   corresponding to  proposed solution 2,  as shown in the adjacent calculation.
  • But additionally the  proposed solution 3  is correct,  because one recognizes from this calculation scheme further following periodicities of the impulse response  g_   (up to infinity)  because of in each case same register assignment:
g3 = g6=g9=...=1,
g4 = g7=g10=...=0,
g5 = g8=g11=...=1.





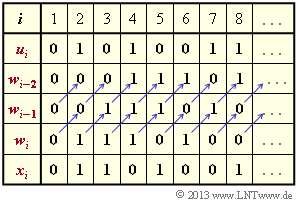
(2) After similar calculations as in subtask  (1)  one recognizes the correctness of  solutions 1 and 3:

  • The initial sequence  x_  also extends to infinity.  Periodicities show up again.
  • The same result is obtained by adding the impulse responses   g_=(1,0,1,0,1,1,0,1,...)   in the Galois field  GF(2)  shifted by one,  three,  six,  and seven positions  (to the right,  respectively):
x_=(0,1,1,1,0,1,1,0,...)+(0,0,0,1,1,1,0,1,...)+(0,0,0,0,0,0,1,1,...)+(0,0,0,0,0,0,0,1,...)
⇒x_=(0,1,1,0,1,0,0,1,...).
  • Due to the linearity of the system under consideration,  this is allowed.


(3)  Here we choose the way over the D–transforms:

u_=(1,1,1)∘−−D−∙U(D)=1+D+D2.
  • With the transfer function   G(D)=(1+D2)/(1+D+D2)   one thus obtains for the D–transform of the output sequence:
X(D)=U(D)⋅G(D)=1+D+D2⋅1+D21+D+D2=1+D2⇒x_=(1,0,1,0,0,0,...).
  • Only the  proposed solution 1  is correct here:  Despite infinitely long impulse response  g_,  for this input sequence  u_  the output sequence  x_  is limited to three bits.
  • The same result is again obtained by adding shifted impulse responses:
x_=(1,1,1,0,1,1,0,1,...)+(0,1,1,1,0,1,1,0,...)+(0,0,1,1,1,0,1,1,...)=(1,0,1,0,0,0,0,0,...).


(4)  Correct are the  proposed solutions 1 and 3:

  • On the data sheet,  the general transfer function of a second–order recursive filter is given as follows.
GF(2)  polynomial division  (1+D2)/(1+D+D2)
G(D)=a0+a1⋅D+a2⋅D21+b1⋅D+b2⋅D2.
  • The filter considered here is determined by the coefficients  a0=a2=b1=b2=1  and  a1=0.  Thus one obtains the result according to the  solution suggestion 1:
G(D)=1+D21+D+D2.
  • At the same time,  G(D)  is also the D–transformed of the impulse response:
g_=(1,1,1,0,1,1,0, ...)∘−−D−∙G(D)
⇒G(D)=1+D+D2+D4+D5+....
  • This means:  The  proposed solution 3  is also correct.
  • The same result would have been obtained by dividing the two polynomials  1+D2  and  1+D+D2,  as the calculation opposite shows.

Retrieved from "http://en.lntwww.de/index.php?title=Aufgaben:Exercise_3.5:_Recursive_Filters_for_GF(2)&oldid=50006"
  • Powered by MediaWiki