Exercise 3.6: Transient Behavior

Cosine and sine waves, each causal

In this exercise, we consider a cosine signal $c(t)$ with amplitude $1$ and period $T = 1 \ \rm µ s$, which is defined for all times $t$ $($in the range $ \pm \infty)$ :

$$c(t) = \cos(2\pi \cdot {t}/{T}) \hspace{0.05cm} .$$

The causal $($German: "kausal" ⇒ subscript "K"$)$ cosine signal $c_{\rm K}(t)$ (red curve) starts only at the turn-on instant $t = 0$:

$$c_{\rm K}(t)= \left\{ \begin{array}{c} c(t) \\ 0 \end{array} \right. \begin{array}{c} {\rm{for}} \\ {\rm{for}} \end{array}\begin{array}{*{20}c} { t \ge 0\hspace{0.05cm},} \\ { t < 0\hspace{0.05cm}.} \end{array}$$

Only the Fourier spectrum can be specified for the bilaterally unbounded signal $c(t)$:

$$C(f) = {1}/{ 2} \cdot \delta (f - f_0) + {1}/{ 2} \cdot \delta (f + f_0) \quad {\rm with} \quad f_0 = {1}/{ T}= 1\,\,{\rm MHz.}$$

On the contrary, for the causal cosine signal $c_{\rm K}(t)$ the Laplace transform can also be specified:

$$C_{\rm L}(p) = \frac {p} { (p-{\rm j} \cdot 2 \pi/T)\cdot (p+{\rm j} \cdot 2 \pi/T)}\hspace{0.05cm} .$$

Accordingly, the following holds for the Laplace transform of the causal sine function $s_{\rm K}(t)$:

$$S_{\rm L}(p) = \frac {2 \pi/T} { (p-{\rm j} \cdot 2 \pi/T)\cdot (p+{\rm j} \cdot 2 \pi/T)}\hspace{0.05cm} .$$

The bilaterally unbounded sine function is denoted by $s(t)$ and is shown as a blue–dotted curve in the below diagram.

The signals $c(t)$, $c_{\rm K}(t)$, $s(t)$ and $s_{\rm K}(t)$ are applied to the input of a low-pass filter of first-order with the following transfer function (or impulse response):

$$H_{\rm L}(p) = \frac {2 /T} { p + 2 /T} \quad \bullet\!\!-\!\!\!-^{\hspace{-0.25cm}\rm L}\!\!\!-\!\!\circ\quad h(t) = {2}/{T} \cdot {\rm e}^{\hspace{0.05cm}-\hspace{0.03cm}2 \hspace{0.03cm}t/T}.$$

The corresponding output signals are denoted by $y_{\rm C}(t)$, $y_{\rm CK}(t)$, $y_{\rm S}(t)$ and $y_{\rm SK}(t)$ .
These signals are to be computed and correlated to each other in this exercise.

Please note:

The exercise belongs to the chapter Inverse Laplace Transform.
The computations for subtask (6) are bulky.
For computing the signals $y_{\rm CK}(t)$ and $y_{\rm SK}(t)$, for example the residue theorem can be used.

Questions

$|H(f = f_0)| \ = \ $

$a(f = f_0)\hspace{0.2cm} = \ $

$\ \rm Np$

${\rm arc} \ H(f = f_0)\ = \ $

$\ \rm deg$

$b(f = f_0)\hspace{0.24cm} = \ $

$\ \rm deg$

$y_{\rm C}(t = 0) \ = \ $

$y_{\rm S}(t = 0) \ = \ $

$T_h/T \ = \ $

	The following holds: $y_{\rm CK}(t) \equiv 0$ and $y_{\rm SK}(t) \equiv 0$ for $t < 0$.
	The signal $y_{\rm CK}(t)$ is approximately equal to $y_{\rm C}(t)$ for $t > T_h$ .
	The causal signal $y_{\rm SK}(t)$ is approximately equal to $y_{\rm S}(t)$ for $t < T_h$ .

$y_\text{CK}(t = T/5) \ = \ $

Solution

(1) Replacing the parameter $T$ by $1/f_0$ and $p$ by ${\rm j} \cdot 2 \pi f$ in $H_{\rm L}(p)$ the following is obtained for the frequency response in general or for $f_0 = 1 \ \rm MHz$:

$$H(f) = \frac {2 /T} { {\rm j} \cdot 2 \pi f + 2 /T}= \frac {f_0} { {\rm j} \cdot \pi f + f_0} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} H(f= f_0) = \frac {1} { 1 + {\rm j} \cdot \pi }$$

$$\Rightarrow \hspace{0.3cm} |H(f= f_0)| = \frac {1} { \sqrt{1 + \pi^2 }} \hspace{0.15cm}\underline{= 0.303}\hspace{0.05cm},\hspace{0.2cm}a(f= f_0)= - {\rm ln}\,\, |H(f= f_0)| \hspace{0.15cm}\underline{\approx 1.194\,\,{\rm Np}}$$

$$\Rightarrow \hspace{0.3cm} {\rm arc}\,H(f= f_0)= - {\rm arctan}\,(\pi) \hspace{0.15cm}\underline{\approx -72^\circ} \hspace{0.05cm}, \hspace{0.2cm}b(f= f_0)= -{\rm arc}\,H(f= f_0) \hspace{0.15cm}\underline{\approx +72^\circ} \hspace{0.05cm}.$$

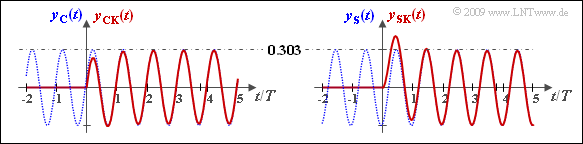
(2) The output signal $y_{\rm C}(t)$ is attenuated by the factor $0.303$ and delayed by $\tau \approx 72/360 \cdot T = T/5$ compared to the input signal $c(t)$ .

Thus, this signal can also be described as follows:

$$y_{\rm C}(t) = \frac { \cos(2\pi {t}/{T}) + \pi \cdot \sin(2\pi {t}/{T})} { {1 + \pi^2 }}= 0.303 \cdot \cos(2\pi \cdot \frac{t-T/5}{T}) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} y_{\rm C}(t=0) = \frac {1} { {1 + \pi^2 }} \hspace{0.15cm}\underline{\approx 0.092} \hspace{0.05cm}.$$

This signal is shown dotted in blue in the left graph for solution (5).

(3) The signal $y_{\rm S}(t)$ is also smaller by the attenuation factor $0.303$ and delayed by the time period $\tau = T/5$ compared to $s(t)$ .

It can be described as follows:

$$y_{\rm S}(t) = \frac { -\pi \cdot \cos(2\pi {t}/{T}) + \sin(2\pi {t}/{T})} { {1 + \pi^2 }}= 0.303 \cdot \sin(2\pi \cdot \frac{t-T/5}{T}) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} y_{\rm S}(t=0) = -\frac {\pi} { {1 + \pi^2 }} \hspace{0.15cm}\underline{\approx -0.289} \hspace{0.05cm}.$$

This signal is sketched dotted in blue in the right graph for solution (5) .

(4) At $T_h$ the impulse response $h(t)$ should have decayed to $1\%$ of the maximum value. Thus, the following holds:

$${\rm e}^{\hspace{0.05cm}-\hspace{0.03cm}2 \hspace{0.03cm}T_{ h}/T} = 0.01 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {T_{ h}}/{T} =\frac{1}{2} \cdot {\rm ln}\,\, \frac{1}{0.01} \hspace{0.15cm}\underline{\approx 2.3} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}h(t=0) = {2}/{T}\hspace{0.05cm}, \hspace{0.2cm}h(t=T_{ h}) = {0.02}/{T}\hspace{0.05cm}.$$

Transient behavior of a causal cosine and a causal sine signal

(5) The statements 1 and 2 are correct:

The causal signals $y_{\rm CK}(t)$ and $y_{\rm SK}(t)$ must be identical to zero for $t < 0$ .
However, since the impulse response $h(t)$ of the considered filter (nearly) vanishes for $t > T_h$, it does not matter whether the unbounded cosine signal $c(t)$ or the causal signal $c_{\rm K}(t)$ is applied to the input after the transient effect is over.
The same is true for the sinusoidal signals: For $t >T_{ h}$, $y_{\rm SK}(t)=y_{\rm S}(t)$ holds.

The graph shows the output signals $y_{\rm C}(t)$ and $y_{\rm CK}(t)$ for cosine-shaped input on the left and the signals $y_{\rm S}(t)$ and $y_{\rm SK}(t)$ for sinusoidal input on the right. Note the transit time of $T/5$ $($corresponding to the phase $72^\circ)$ in both cases.

For $y_{\rm CK}(t)$ the first wave peaks are smaller than $1$ to achieve the correct phase position of $y_{\rm C}(t)$ .
In contrast, for $y_{\rm SK}(t)$ the first wave peaks are greater than $1$ to achieve the correct phase position of $y_{\rm S}(t)$ .

(6) Considering $p_{\rm x1}= {\rm j} \cdot {2\pi}/{T} , \hspace{0.1cm}p_{\rm x2}= -{\rm j} \cdot {2\pi}/{T} , \hspace{0.1cm} p_{\rm x3}= -{2}/{T} \hspace{0.05cm}$ the following can be written for the Laplace transform of the signal $y_{\rm CK}(t)$ :

$$Y_{\rm L}(p) = \frac {-p_{{\rm x}3}\cdot p} { (p-p_{{\rm x}1})(p-p_{{\rm x}2})(p-p_{{\rm x}3})} \hspace{0.05cm}.$$

The time function $y_{\rm CK}(t)$ is thus composed of three parts according to the residue theorem:

Considering $p_{\rm x2}= -p_{\rm x1}$ the first part is

$$y_1(t)= {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}1}} \hspace{0.05cm}\{Y_{\rm L}(p)\cdot {\rm e}^{\hspace{0.03cm}p t}\}= \frac {-p_{{\rm x}3}\cdot p} { (p-p_{{\rm x}2})(p-p_{{\rm x}3})}\cdot {\rm e}^{\hspace{0.03cm}p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}1}}= \frac {-p_{{\rm x}3}\cdot p_{{\rm x}1}} { (p_{{\rm x}1}-p_{{\rm x}2})(p_{{\rm x}1}-p_{{\rm x}3})}\cdot {\rm e}^{\hspace{0.03cm}p_{{\rm x}1}\cdot \hspace{0.03cm}t}= \frac {-p_{{\rm x}3}/2} { p_{{\rm x}1}-p_{{\rm x}3}}\cdot {\rm e}^{\hspace{0.03cm}p_{{\rm x}1}\cdot \hspace{0.03cm}t} \hspace{0.05cm} .$$

Similarly, the following is obtained for the second part:

$$y_2(t)= {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}2}} \hspace{0.05cm}\{Y_{\rm L}(p)\cdot {\rm e}^{\hspace{0.03cm}p t}\}= \frac {-p_{{\rm x}3}\cdot p} { (p-p_{{\rm x}1})(p-p_{{\rm x}3})}\cdot {\rm e}^{\hspace{0.03cm}p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}2}}=\frac {-p_{{\rm x}3}\cdot p_{{\rm x}2}} { (p_{{\rm x}2}-p_{{\rm x}1})(p_{{\rm x}2}-p_{{\rm x}3})}\cdot {\rm e}^{\hspace{0.03cm}p_{{\rm x}2}\cdot \hspace{0.03cm}t}= \frac {p_{{\rm x}3}/2} { p_{{\rm x}1}+p_{{\rm x}3}}\cdot {\rm e}^{-p_{{\rm x}1}\cdot \hspace{0.03cm}t} \hspace{0.05cm} .$$

Combining both parts and considering the numerical values of $p_{\rm x1}$ and $p_{\rm x3}$:

$$y_{1\hspace{0.03cm}+2}(t)= \frac {1/T} { 2/T + {\rm j} \cdot 2\pi /T} \cdot {\rm e}^{\hspace{0.03cm}{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi \hspace{0.03cm} t/T}+\frac {1/T} { 2/T - {\rm j} \cdot 2\pi /T} \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi \hspace{0.03cm}t/T}= \frac {1/2} { 1 + {\rm j} \cdot \pi } \cdot {\rm e}^{\hspace{0.03cm}{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi \hspace{0.03cm}t/T}+\frac {1/2} { 1 - {\rm j} \cdot \pi } \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi \hspace{0.03cm}t/T}$$

$$\Rightarrow \hspace{0.3cm} y_{1\hspace{0.03cm}+2}(t)\hspace{0.25cm} = \frac {1/2 \cdot (1 - {\rm j} \cdot \pi)} { 1 + \pi^2 } \cdot {\rm e}^{\hspace{0.03cm}{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi \hspace{0.03cm}t/T}+\frac {1/2 \cdot (1 + {\rm j} \cdot \pi)} { 1 + \pi^2 } \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi \hspace{0.03cm}t/T} \hspace{0.05cm} $$

Using Euler's theorem this can also be expressed as follows:

$$y_{1\hspace{-0.03cm}+2} (t) = \frac { \cos(2\pi {t}/{T}) + \pi \cdot \sin(2\pi {t}/{T})} { {1 + \pi^2 }}= y_{\rm C}(t)\hspace{0.05cm}.$$

It can be seen that $y_{1\hspace{0.03cm}+2}(t)$ is equal to the signal $y_{\rm C}(t)$ computed in subtask (2) .

Finally, the following is obtained for the last residual:

$$y_3(t)=\frac {-p_{{\rm x}3}^2} { (p_{{\rm x}3}-p_{{\rm x}1}) (p_{{\rm x}3}-p_{{\rm x}2})} \cdot {\rm e}^{\hspace{0.05cm}p_{{\rm x}3}\cdot \hspace{0.03cm}t}= \frac {-(2/T)^2 \cdot {\rm e}^{\hspace{0.05cm}-2 \hspace{0.03cm}t/T}} { (-2/T-{\rm j} \cdot 2\pi /T) (-2/T+{\rm j} \cdot 2\pi /T)} =\frac {- {\rm e}^{\hspace{0.05cm}-2 \hspace{0.03cm}t/T} } { (1+{\rm j} \cdot \pi ) (1-{\rm j} \cdot \pi)} =\frac {- {\rm e}^{\hspace{0.05cm}-2 \hspace{0.03cm}t/T}} { 1+\pi^2} \hspace{0.05cm} .$$

Thus, the output signal is as follows for a causal cosine signal applied to the input:

$$y_{\rm CK}(t) = y_1(t)+y_2(t)+y_3(t) = \frac { \cos(2\pi {t}/{T}) + \pi \cdot \sin(2\pi {t}/{T})-{\rm e}^{\hspace{0.05cm}-2 \hspace{0.03cm}t/T}} { {1 + \pi^2 }}$$

$$\Rightarrow \hspace{0.3cm}y_{\rm CK}(t = {T}/{5}) = \frac { \cos(72^\circ) + \pi \cdot \sin(72^\circ)-{\rm e}^{\hspace{0.05cm}-0.4}} { {1 + \pi^2 }} \hspace{0.15cm}\underline{ \approx 0.24} < 0.303\hspace{0.05cm} .$$

For comparison: The signal $y_{\rm C}(t)$ has the value $0.303$ at this time.

In contrast to this, the following arises as a result in general and specifically at the time of the first maximum at $t = 0.45 \cdot T$ for the causal sinusoidal signal applied to the input:

$$y_{\rm SK}(t) = \frac { -\pi \cdot \cos(2\pi {t}/{T}) + \sin(2\pi {t}/{T})+\pi \cdot {\rm e}^{\hspace{0.05cm}-2 \hspace{0.03cm}t/T}} { {1 + \pi^2 }}$$

$$\Rightarrow \hspace{0.3cm} y_{\rm SK}(t = 0.45 \cdot T) = \frac { -\pi \cdot \cos(162^\circ) + \sin(162^\circ)+\pi \cdot{\rm e}^{\hspace{0.05cm}-0.9}} { {1 + \pi^2 }} \approx 0.42 > 0.303\hspace{0.05cm} .$$