Exercise 3.7: Impulse Response of a High-Pass Filter

High-pass filter of second-order

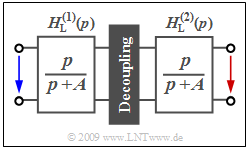
We assume the sketched arrangement. The transfer functions of the two identical high-pass filters are:

$$H_{\rm L}^{(1)}(p) = H_{\rm L}^{(2)}(p) =\frac{p}{p+A} \hspace{0.05cm} .$$

Since the two-port networks are decoupled in terms of resistance by an isolation amplifier, the total transfer function can be written as follows:

$$H_{\rm L}(p) = H_{\rm L}^{(1)}(p) \cdot H_{\rm L}^{(2)}(p) \hspace{0.05cm} .$$

At the same time it is known that the following equation is valid:

$$H_{\rm L}(p) =\frac{4}{1/p^2 + 4/p +4} \hspace{0.05cm} .$$

If this function is represented in pole–zero notation, it will turn out that here the number of zeros $(Z)$ is equal to the number of poles $(N)$ . Therefore, a direct application of the residue theorem is not possible here.

Instead, in order to compute the time function $h(t)$ a partial fraction decomposition corresponding to $H_{\rm L}(p) =1- H_{\rm L}\hspace{-0.05cm}'(p) \hspace{0.05cm}$ must be made. Thus, the following holds for the impulse response:

$$h(t) = \delta(t)- h\hspace{0.03cm}'(t) \hspace{0.05cm}.$$

$Z' < N'$ holds with respect to $H_{\rm L}'(p)$. Thus, the continuous component $h'(t)$ of the impulse response can be determined using the residue theorem.

Please note:

The exercise belongs to the chapter Inverse Laplace Transform.
The residual of an $l$–fold pole $p_{\rm x}$ within the function $H_{\rm L}(p)$ is:

$${\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{\rm x}} \hspace{0.03cm}\{H_{\rm L}(p)\cdot {\rm e}^{\hspace{0.05cm}p t}\}= \frac{1}{(l-1)!}\cdot \frac{{\rm d}^{\hspace{0.05cm}l-1}}{{\rm d}p^{\hspace{0.05cm}l-1}}\hspace{0.15cm} \left \{H_{\rm L}(p)\cdot (p - p_{\rm x})^{\hspace{0.05cm}l} \cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}t}\right\} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{\rm x}} \hspace{0.05cm} .$$

The derivative of the product $y(x) = f(x) \cdot g(x)$ is given as follows:

$$\frac{{\rm d}{\hspace{0.05cm}y(x)}}{{\rm d}\hspace{0.05cm}x}= \frac{{\rm d}{\hspace{0.05cm}f(x)}}{{\rm d}\hspace{0.05cm}x}\cdot g(x) + \frac{{\rm d}{\hspace{0.05cm}g(x)}}{{\rm d}\hspace{0.05cm}x}\cdot f(x) \hspace{0.05cm} .$$

Questions

$Z \hspace{0.28cm} = \ $

$N \hspace{0.2cm} = \ $

$K \hspace{0.2cm} = \ $

$A \ = \ $

	$H_{\rm L}'(p) = p^2/(p+0.5)^2$,
	$H_{\rm L}'(p) = p/(p+0.5)^2$,
	$H_{\rm L}'(p) = (p+0.25)/(p+0.5)^2$.

$h'(t = 0) \ = \ $

$h'(t = 1) \ = \ $

$h'(t → ∞)\ = \ $

Solution

(1) Starting from the given equation, $H_{\rm L}(p)$ can be transformed as follows:

$$H_{\rm L}(p) =\frac{4}{1/p^2 + 4/p +4}=\frac{p^2}{p^2 + p +1/4}=\frac{p^2}{(p +1/2)^2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \hspace{0.15cm}\underline{ Z = 2\hspace{0.05cm} , \hspace{0.2cm}N = 2\hspace{0.05cm} , \hspace{0.2cm}K = 1} \hspace{0.05cm} .$$

(2) The total transfer function is as follows according to the information page:

$$H_{\rm L}(p) = H_{\rm L}^{(1)}(p) \cdot H_{\rm L}^{(2)}(p) =\frac{p^2}{(p+A)^2} \hspace{0.05cm} .$$

A comparison with the result of subtask (1) shows that $\underline{A = 0.5}$ must hold.

(3) The last suggested solution is correct:

The following is obtained based on the equation computed in subtask (1) :

$$H_{\rm L}(p) =\frac{p^2}{p^2 + p +0.25}= \frac{p^2 + p +0.25}{p^2 + p +0.25}- \frac{p +0.25}{p^2 + p +0.25}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}H_{\rm L}\hspace{-0.05cm}'(p) = \frac{p +0.25}{p^2 + p +0.25}= \frac{p +0.25}{(p +0.5)^2} \hspace{0.05cm} .$$

(4) Concerning the function $H_{\rm L}'(p)$ ⇒ $Z' = 1$, $N' = 2$ and $K' = 1$ hold.

The two poles at $p_{\rm x} = -0.5$ coincide such that only one residual needs to be determined:

$$h\hspace{0.03cm}'(t) \hspace{0.25cm} = \hspace{0.2cm} {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{\rm x}} \hspace{0.7cm}\{H_{\rm L}\hspace{-0.05cm}'(p)\cdot {\rm e}^{p t}\}= \frac{\rm d}{{\rm d}p}\hspace{0.15cm} \left \{ \frac{p +0.25}{(p +0.5)^2} \cdot (p +0.5)^2 \cdot {\rm e}^{p \hspace{0.05cm}t}\right\} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-0.5} = \hspace{0.2cm}\frac{\rm d}{{\rm d}p}\hspace{0.15cm} \left \{ (p +0.25) \cdot {\rm e}^{p \hspace{0.05cm}t}\right\} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-0.5} \hspace{0.05cm} .$$

Impulse response of the high-pass filter including Dirac delta (red);
continuous component $h\hspace{0.03cm}'(t)$ (blue)

The following is obtained using the product rule of differential calculus:

$$h\hspace{0.03cm}'(t) \hspace{0.15cm} = \hspace{0.15cm} {\rm e}^{p \hspace{0.05cm}t} + ( p + 0.25) \cdot t \cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-0.5} = \hspace{0.15cm} (1- {t}/{4}) \cdot{\rm e}^{-t/2} \hspace{0.05cm} $$

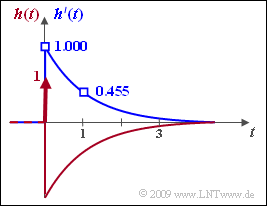
$$\Rightarrow \hspace{0.3cm}h\hspace{0.03cm}'(t = 0) \hspace{0.15cm} = \underline{1}\hspace{0.05cm} ,\hspace{0.3cm} h\hspace{0.03cm}'(t = 1) \hspace{0.15cm} = \underline {0.455}\hspace{0.05cm} \hspace{0.05cm} ,\hspace{0.3cm} h\hspace{0.03cm}'(t \rightarrow \infty) \hspace{0.15cm} = \underline {= 0}\hspace{0.05cm} .$$

The graph shows in each case for non–negative times

the impulse response $h'(t)$ of the equivalent low-pass filter as a blue curve,
the total impulse response of the considered high-pass filter as a red curve:

$$h(t) = \delta (t) - (1- {t}/{4}) \cdot{\rm e}^{-t/2} \hspace{0.05cm}.$$