Exercise 3.8: Delay Filter DFE Realization
We consider a bipolar binary system with decision feedback equalization $\rm (DFE)$.
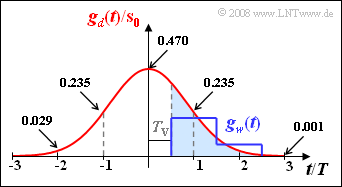
The pre-equalized basic pulse $g_d(t)$ can be calculated as the rectangular response of a Gaussian low-pass filter with the cutoff frequency $f_{\rm G} \cdot T = 0.25$ and is shown in red in the diagram. In Exercise 3.8Z the samples of $g_d(t)$ are tabulated in the distance $T/10$.
With ideal decision feedback – dimensioned for the detection time $T_{\rm D} = 0$ – applies:
- A compensation pulse $g_w(t)$ is formed, which is equal to $g_d(t)$ for $t ≥ T_{\rm V} = T/2$ and identical to zero for $t < T_{\rm V}$ (blue filled area).
- The corrected basic pulse $g_k(t) = g_d(t) - g_w(t)$ is thus always zero for $t > T/2$.
By simulation, the worst-case S/N ratio at the decision and from this the worst–case error probability were determined for this system with ideal DFE and with detection at time $T_{\rm D} = 0$. The result was as follows:
- $$\rho_{\rm U} = \frac{\big[\ddot{o}(T_{\rm D})/2\big]^2}{ \sigma_d^2} = 25 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} \approx 14\,{\rm dB} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm U} = {\rm Q}(\sqrt{\rho_{\rm U}}) \approx 2.9 \cdot 10^{-7} \hspace{0.05cm}.$$
A low-effort realization of the DFE is possible with a delay filter. In the graph, the compensation pulse $g_w(t)$ for such a delay filter with order $N = 2$ and coefficients $k_1 = 0.2$ and $k_2 = 0.05$ is plotted (blue curve).
Note: The exercise belongs to the chapter "Decision Feedback".
Questions
Solution
- $$\frac{\ddot{o}(T_{\rm D})}{ 2} = g_d(0) - g_d(-T)- g_d(-2T)- g_d(-3T)\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \frac{\ddot{o}(T_{\rm D})}{ 2 \cdot s_0} = 0.470 - 0.235 - 0.029 -0.001\hspace{0.15cm}\underline { = 0.205} \hspace{0.05cm}.$$
(2) From the given worst-case S/N ratio $\rho_{\rm U} = 25$, it follows:
- $$\rho_{\rm U} = \frac{[\ddot{o}(T_{\rm D})/2]^2}{ \sigma_d^2} = 25 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} (\sigma_d/s_0)^2 = \frac{[\ddot{o}(T_{\rm D})/(2s_0)]^2}{ 25}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \sigma_d/s_0 = \frac{\ddot{o}(T_{\rm D})/(2s_0)}{ 5} \hspace{0.15cm}\underline {= 0.041} \hspace{0.05cm}.$$
(3) By this filter, the first two trailers are only partially compensated and the third trailer is not compensated at all.
- From this follows with the result of subtask (1):
- $$\frac{\ddot{o}(T_{\rm D})}{ 2 \cdot s_0} \ = \ 0.205 - | 0.235 - 0.2 | - |0.029 -0.05 | -0.001 = 0.205 - 0.035 - 0.021 -0.001 \hspace{0.15cm}\underline {= 0.148}$$
- $$\Rightarrow \hspace{0.3cm} \rho_{\rm U} =\frac{0.148^2}{ 0.041^2} \approx 13 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U}\hspace{0.15cm}\underline { \approx 11.1\,{\rm dB}} \hspace{0.05cm}.$$
(4) Almost the same results are obtained as for ideal DFE (only the third trailer is not compensated):
- $$\frac{\ddot{o}(T_{\rm D})}{ 2 \cdot s_0}\hspace{0.15cm}\underline { = 0.204} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} \hspace{0.15cm}\underline {\approx 13.94 \,{\rm dB}}\hspace{0.3cm}{\rm (Ideal \hspace{0.15cm}DFE\hspace{-0.15cm}:}\hspace{0.15cm}{13.98 \,{\rm dB)}} \hspace{0.05cm}.$$
(5) The first two statements are correct:
- Without DFE, the half eye opening is:
- $$\frac{\ddot{o}(T_{\rm D})}{ 2 \cdot s_0} = 0.470 - 2 \cdot 0.235 - 2 \cdot 0.029 - 2 \cdot 0.001 < 0 \hspace{0.05cm}.$$
- If at some point a wrong decision is made due to a too large noise component, the falsification probability of the subsequent symbols is significantly increased. However, there are always symbol combinations in each sequence that interrupt this propagation of uncertainty.
- The last statement is wrong. It is rather true: Small distances from the decision threshold are increased, large distances, on the other hand, are decreased and their falsification probabilities are consequently increased. On average, however, this leads to a smaller error probability.