Exercise 3.9: Characteristic Curve for Cosine PDF
From LNTwww
We are looking for a continuous, monotonically increasing nonlinear characteristic $y =g(x)$, which generates a new random variable with "cosine" PDF from a between $-1$ and $+1$ uniformly distributed random variable $x$:
- $$f_y(y)=A\cdot\cos({\pi}/{2}\cdot y).$$
- The random variable $y$ can also only take values between $-1$ and $+1$.
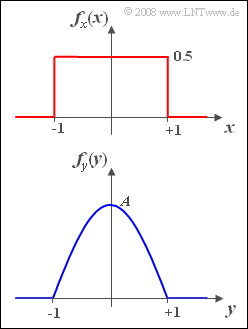
- The two density functions $f_x(x)$ and $f_y(y)$ are sketched on the right.
Hints:
- The exercise belongs to the chapter Exponentially Distributed Random Variables.
- In particular, reference is made to the page Transformation of random variables.
Question
Solution
(1) Correct are the statements 1 and 3:
- Since $x$ can only take values between $\pm 1$, the course of the characteristic curve outside of this range is irrelevant for the random variable $y$.
- The condition $g(-x) = g(x)$ does not have to be met. There are any number of characteristic curves that can generate the desired PDF.
- For example, the characteristic curve calculated in point (5) is point-symmetric: $g(-x) = -g(x)$.
- The graphical representations of the two density functions already show that $\sigma_y^2 < \sigma_x^2$.
(2) The integral over the PDF must always equal $1$ . It follows that:
- $$\int_{-\rm 1}^{\rm 1}A\cdot \cos({\pi}/{\rm 2}\cdot y)\, {\rm d} y=\frac{A\cdot \rm 4}{\pi}\hspace{0.3cm} \rightarrow\hspace{0.3cm} A=\frac{\pi}{\rm 4} \hspace{0.15cm}\underline{= \rm 0.785}.$$
(3) The transformation formula can be described as follows:
- $$f_y(y)=\frac{f_x(x)}{| g'(x)|}\Big|_{\, x=h(y)}=f_x(x)\cdot |h'(y)| \Big|_{\, x=h(y)}.$$
- The inverse function $x = h(y)$ of a monotonically increasing characteristic $y = g(x)$ also increases monotonically.
- Therefore one does not need to make use of the absolute value and subsequently obtains:
- $$h\hspace{0.05cm}'(y)=\frac{f_y(y)}{f_x(x)\Big|_{\, x=h(y)}}={\pi}/{\rm 2}\cdot \cos({\pi}/{2}\cdot y).$$
- At the point $y = 0$ the slope has the value $h\hspace{0.05cm}'(y= 0)=π/2\hspace{0.15cm}\underline{\approx 1.571}$.
(4) One obtains by (indefinite) integration:
- $$h(y)=\int h\hspace{0.05cm}'(y)\, {\rm d} y + C = \frac{\pi}{2}\cdot \frac{2}{\pi}\cdot \sin(\frac{\pi}{ 2}\cdot y) + C.$$
- The constraint $h(y= 0) = 0$ leads to the constant $C = 0$ and thus to the result:
- $$h(y) = \sin({\pi}/{2}\cdot y) \hspace{0.5cm} \rightarrow\hspace{0.5cm} h(y = 1) \hspace{0.15cm}\underline{= +1}.$$
(5) The inverse function of the function determined in subtask (4) is $x = h(y)$ :
- $$y=g(x)={\rm 2}/{\rm \pi}\cdot \rm arcsin({\it x}).$$
- This characteristic curve increases monotonically in the range $-1 \le x \le +1$ from $y = -1$ to $y = +1$ .
- So the value we are looking for is $g(x= 1) \hspace{0.15cm}\underline{= +1}$.