Exercise 4.11Z: OOK and BPSK once again
The error probabilities $p_{\rm S}$ of the digital modulation methods "On–Off Keying" $\rm (OOK)$ and "Binary Phase Shift Keying" $\rm (BPSK)$ are given here without derivation.
For example, one obtains with the so-called Q-function
- $${\rm Q} (x) = \frac{\rm 1}{\sqrt{\rm 2\pi}}\cdot \int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}/\rm 2}\,d \it u$$
for the AWGN channel – identified by $E_{\rm S}/N_0$ – and other optimal conditions (e.g. coherent demodulation)
- for On–Off Keying, often also called "Amplitude Shift Keying" $\rm (2–ASK)$:
- $$p_{\rm S} = {\rm Q}\left ( \sqrt{{E_{\rm S}}/{N_0 }} \hspace{0.1cm}\right ) \hspace{0.05cm},$$
- for Binary Phase Shift Keying:
- $$p_{\rm S} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm S}}/{N_0 }} \hspace{0.1cm}\right ) \hspace{0.05cm}.$$
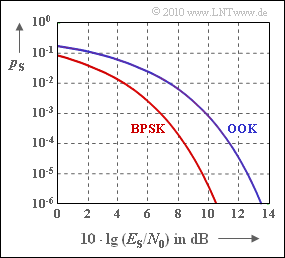
These symbol error probabilities (at the same time the bit error probabilities) are shown in the graph.
For example, for $10 \cdot {\rm lg} \, E_{\rm S}/N_0 = 10 \ \rm dB$ one obtains according to the exact functions:
- $$p_{\rm S} = 7.83 \cdot 10^{-4}\,\,{\rm (OOK)}\hspace{0.05cm},$$
- $$ p_{\rm S} = 3.87 \cdot 10^{-6}\,\,{\rm (BPSK)}\hspace{0.05cm}.$$
In order to achieve $p_{\rm S} = 10^{\rm -5}$ with BPSK, $10 \cdot {\rm lg} \, E_{\rm S}/N_0 ≥ 9.6 \ \rm dB$ must hold.
Notes:
- The exercise belongs to the chapter "Carrier Frequency Systems with Coherent Demodulation".
- You can also find the derivations in the chapter "Linear Digital Modulation – Coherent Demodulation".
- For the complementary Gaussian error function, use the following approximation (upper bound):
- $${\rm Q}(x) \approx \frac{1}{\sqrt{2\pi} \cdot x} \cdot {\rm e}^{-x^2/2} \hspace{0.05cm}.$$
Questions
Solution
- $$p_{\rm S} = {\rm Q}\left ( \sqrt{10} \right ) \approx \frac{\rm 1}{\sqrt{\rm 20\pi} }\cdot \rm e^{-5 } \underline{=85 \cdot 10^{-5}}\hspace{0.05cm}.$$
- The actual value according to the data section is $78.3 \cdot 10^{\rm -5}$.
- So the given equation is actually an upper bound for ${\rm Q}(x)$.
- The relative error when using this approximation instead of the exact function ${\rm Q}(x)$ is in this case less than $10\%$.
(2) For BPSK, the corresponding equation is:
- $$p_{\rm S} = {\rm Q}\left ( \sqrt{20} \right ) \approx \frac{\rm 1}{\sqrt{\rm 40\pi} }\cdot \rm e^{-10 } \underline{=0.405 \cdot 10^{-5}}\hspace{0.05cm}.$$
- Now the relative error using the approximation is only $5\%$.
- In general: The smaller the error probability, the better the approximation.
(3) According to the specification, a (logarithmic) value of $9.6 \ \rm dB$ is required for BPSK.
- With the OOK, the logarithmic value must be increased by about $3 \ \rm dB$ ⇒ $10 \cdot {\rm lg} \, E_{\rm S}/N_0 \ \underline {\approx 12.6 \ \rm dB}$.