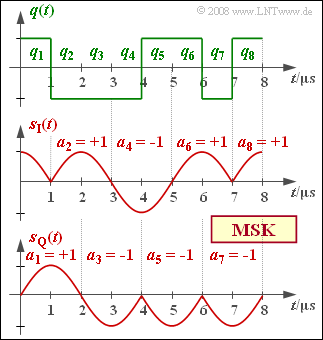
Exercise 4.14: Phase Progression of the MSK
One possible implementation of Minimum Shift Keying $\rm (MSK)$ is offered by $\rm Offset–QPSK$, as shown in the block diagram in the theory section.
- For this, a recoding of the source symbols $q_k ∈ \{+1, –1\}$ into the similarly binary amplitude coefficients $a_k ∈ \{+1, –1\}$ must first be undertaken.
- This recoding is discussed in detail in Exercise 4.14Z .
The graph shows the two equivalent low-pass signals $s_{\rm I}(t)$ and $s_{\rm Q}(t)$ in the two branches below, which are obtained for the inphase and quadrature branches after recoding $a_k = (-1)^{k+1} \cdot a_{k-1} \cdot q_k $ from the source signal $q(t)$ sketched above. Considered here is the MSK fundamental pulse,
- $$ g_{\rm MSK}(t) = \left\{ \begin{array}{l} \cos \big ({\pi \hspace{0.05cm} t}/({2 \hspace{0.05cm} T})\big ) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{for}} \\{\rm{for}} \\ \end{array}\begin{array}{*{10}c} -T \le t \le +T \hspace{0.05cm}, \\ {\rm otherwise}\hspace{0.05cm}. \\ \end{array}$$
This is normalized to $1$ , as are the signals $s_{\rm I}(t)$ and $s_{\rm Q}(t)$ .
In keeping with the chapter Equivalent Low-Pass Signal and its Spectral Function in the book "Signal Representation", the equivalent low-pass signal is:
- $$ s_{\rm TP}(t) = s_{\rm I}(t) + {\rm j} \cdot s_{\rm Q}(t) = |s_{\rm TP}(t)| \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}\phi(t)}\hspace{0.05cm},$$
- with magnitude
- $$|s_{\rm TP}(t)| = \sqrt{s_{\rm I}^2(t) + s_{\rm Q}^2(t)} $$
- and phase
- $$ \phi(t) = {\rm arc} \hspace{0.15cm}s_{\rm TP}(t) = {\rm arctan}\hspace{0.1cm} \frac{s_{\rm Q}(t)}{s_{\rm I}(t)} \hspace{0.05cm}.$$
The physical MSK transmitted signal is then given by
- $$ s(t) = |s_{\rm TP}(t)| \cdot \cos (2 \pi \cdot f_{\rm T} \cdot t + \phi(t)) \hspace{0.05cm}.$$
Hints:
- This exercise belongs to the chapter Nonlinear Digital Modulation.
- Particular reference is made to the section Realizing MSK as Offset–QPSK.
- Assume $ϕ(t = 0) = ϕ_0 = 0$ .
Questions
Solution
- For example, in the range $0 ≤ t ≤ T$, considering that $a_0^2 = a_1^2 = 1$ :
- $$ |s_{\rm TP}(t)| = \sqrt{a_0^2 \cdot \cos^2 (\frac{\pi \cdot t}{2 \cdot T}) + a_1^2 \cdot \sin^2 (\frac{\pi \cdot t}{2 \cdot T})} = 1 \hspace{0.05cm}.$$
- Thus, statement 2 is correct, while statement 1 is false.
- This result holds for any pair of values $a_0 ∈ \{+1, \ –1\}$ and $a_1 ∈ \{+1, \ –1\}$.
- From this, it can be further concluded that the envelope is independent of the transmitted sequence.
(2) With the given equation, it holds that:
- $$\phi(t) = {\rm arctan}\hspace{0.1cm} \frac{s_{\rm Q}(t)}{s_{\rm I}(t)} = {\rm arctan}\hspace{0.1cm} \frac{a_1 \cdot \sin (\frac{\pi \cdot t}{2 \cdot T})}{a_0 \cdot \cos (\frac{\pi \cdot t}{2 \cdot T})}= {\rm arctan}\hspace{0.1cm}\left [ \frac{a_1}{a_0}\cdot \tan \hspace{0.1cm}(\frac{\pi \cdot t}{2 \cdot T})\right ] \hspace{0.05cm}.$$
- The quotient $a_1/a_0$ is always $+1$ or $-1$. Thus, this quotient is preferable and we get:
- $$\phi(t) = \frac{a_1}{a_0}\cdot {\rm arctan}\hspace{0.1cm}\left [ \tan \hspace{0.1cm}(\frac{\pi \cdot t}{2 \cdot T})\right ]= \frac{a_1}{a_0}\cdot \frac{\pi \cdot t}{2 \cdot T} \hspace{0.05cm}.$$
- The initial phase $ϕ_0 = 0$ can rule out ambiguities. In particular, because $a_0 = a_1 = +1$:
- $$\phi(t = T/2 = 0.5\,{\rm µ s}) = {\pi}/{4}\hspace{0.15cm}\underline { = +45^\circ},\hspace{0.2cm}\phi(t = T= 1\,{\rm µ s}) = {\pi}/{2}\hspace{0.15cm}\underline {= +90^\circ} \hspace{0.05cm}.$$
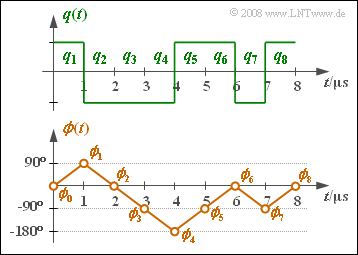
(3) The easiest way to solve this problem is to use the unit circle:
- $$ {\rm Re} = s_{\rm I}(2T) = +1, \hspace{0.2cm} {\rm Im} = s_{\rm Q}(2T) = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\phi(t = 2T= 2\,{\rm µ s}) \hspace{0.15cm}\underline {= 0^\circ},$$
- $$ {\rm Re} = s_{\rm I}(3T) = 0, \hspace{0.2cm} {\rm Im} = s_{\rm Q}(3T) = -1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\phi(t = 3T= 3\,{\rm µ s}) \hspace{0.15cm}\underline {= -90^\circ},$$
- $${\rm Re} = s_{\rm I}(4T) = -1, \hspace{0.2cm} {\rm Im} = s_{\rm Q}(4T) = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\phi(t = 4T= 4\,{\rm µ s})= \pm 180^\circ \hspace{0.05cm}.$$
- From the sketch below, we can see that $\phi(t = 4T= 4\,{\rm µ s})\hspace{0.15cm}\underline { = - 180^\circ}\hspace{0.05cm}$ is correct.
(4) The graph shows the MSK phase $ϕ(t)$ together with the source signal $q(t)$. It can be seen that:
- At symbol $a_\nu =+1$ the phase increases linearly by $90^\circ \ (π/2)$ within the symbol duration $T$ .
- At symbol $a_\nu =-1$ the phase decreases linearly by $90^\circ \ (π/2)$ within the symbol duration $T$ .
- Thus, the remaining phase values are:
- $$\phi(5T) \hspace{0.15cm}\underline { = -90^\circ},\hspace{0.2cm}\phi(t = 6T) \hspace{0.15cm}\underline {= 0^\circ} \hspace{0.05cm}.$$
- $$ \phi(7T)\hspace{0.15cm}\underline { = -90^\circ},\hspace{0.2cm} \phi(t = 8T) \hspace{0.15cm}\underline {= 0^\circ} \hspace{0.05cm}.$$