Exercise 4.16Z: Multi-dimensional Data Reduction

Matrices $\mathbf{K_y}$ and $\mathbf{K_z}$

We consider Gaussian zero mean random variables $\mathbf{x}$, $\mathbf{y}$ and $\mathbf{z}$ with dimensions $N= 1$, $N= 2$ and $N= 3$:

The one-dimensional random variable $\mathbf{x}$ is characterized by the variance $\sigma^2 = 1$ and the standard deviation $\sigma = 1$ respectively.
Because of the dimension $N= 1$ ⇒ $\mathbf{x} = x$.

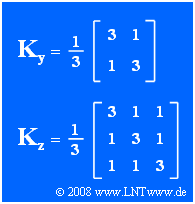
The correlation coefficient between the components $y_1$ and $y_2$ of the 2D random variable $\mathbf{y}$ is $\rho = 1/3$ $($see matrix $\mathbf{K_y})$.
$y_1$ and $y_2$ also have the standard deviation $\sigma = 1$.

The statistics of the three-dimensional random variable $\mathbf{z}$ is completely determined by the correlation matrix $\mathbf{K_z}$ .

If one quantizes the random variable $\mathbf{x}$ in the range between $-4$ and $+4$ with interval width $\Delta_x = 1/32$, there are altogether $N_1 = 256$ different quantization values, for whose transmission thus $n_1 = 8\ \rm {bit}$ would be needed.

Similarly, the random variable $\mathbf{y}$ results in a total of $N_2 = 256^2 = 65536$ different quantized value pairs, if the correlation between $y_1$ and $y_2$ is not taken into account.

Exploiting this correlation – for example, by coordinate transformation from the original system $(y_1, y_2)$ to the new system $(\eta_1, \eta_2)$ – results in a smaller number $N_2\hspace{0.01cm}'$ of quantized value pairs.

Here, it is to be considered that each component is to be quantized according to its respective standard deviation $(\sigma_1$ resp. $\sigma_2)$ in the range of $-4$ to $+4$ and the quantization intervals should be the same in both directions: $\Delta_x = \Delta_y =1/32$.

We denote the quotient $N_2\hspace{0.01cm}'/N_2$ as the data reduction factor with respect to the two-dimensional random variable $\mathbf{y}$.
In analogous definition $N_3'/N_3$ is the corresponding reduction factor of the three-dimensional random variable $\mathbf{z}$ for $\Delta_x = \Delta_y =\Delta_z =1/32.$
Note that in both cases the smallest possible value of this quotient would be favorable.

Hints:

The exercise belongs to the chapter Generalization to N-Dimensional Random Variables.
In particular, reference is made to the section Eigenvalues and Eigenvectors .
Some basics on the application of vectors and matrices can be found on the pages
- Determinant of a Matrix,
- Inverse of a Matrix .
The equation for determination the eigenvalues of $\mathbf{K_z}$ is: $\lambda^3 - 3 \lambda^2 + {24}/{9}\lambda - {20}/{27} = 0.$
One of the three solutions of this equation is $\lambda_1 = 5/3$.

Questions

$\lambda_1 \ = \ $

$\ (\lambda_1 \ge \lambda_2)$

$\lambda_2 \ = \ $

$\ (\lambda_2 \le \lambda_1)$

$N_2\hspace{0.01cm}'/N_2 \ = $

$\lambda_2 \ = \ $

$\ (\lambda_2 \ge \lambda_3)$

$\lambda_3 \ = \ $

$\ (\lambda_3 \le \lambda_2)$

$N_3\hspace{0.01cm}'/N_3 \ = $

Solution

(1) From the condition $\mathbf{K_y} - \lambda \cdot\mathbf{E} = 0$ follows:

$${\rm det}\left[ \begin{array}{cc} 1- \lambda & 1/3 \\ 1/3 & 1- \lambda \end{array} \right] = (1-\lambda)^2 -{1}/{9} = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\lambda^2 -2\lambda+ {8}/{9}= 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\lambda_{1/2}= 1 \pm \sqrt{1-{8}/{9}}= 1 \pm {1}/{3}.$$

The eigenvalues of this $2\times2$ matrix are thus $\lambda_1 = 4/3\hspace{0.15cm}\underline{=1.333}$ and $\lambda_2 = 2/3\hspace{0.15cm}\underline{=0.667}$.

(2) Without considering correlations, there are $N_2 = \left({8}/{ \Delta_x}\right)^2= 256^2 = 65536$ different pairs of values.

Taking into account the correlations and the fact that the two components created by coordinate rotation $\eta_1$ and $\eta_2$ are each in the range $-4\cdot \sigma_1$ to $+4\cdot \sigma_1$ $($resp. from $-4\cdot \sigma_2$ to $+4\cdot \sigma_2)$ ) are to be quantized, one obtains

$$N_2\hspace{0.01cm}' = \frac{8 \hspace{0.05cm}\sigma_1}{\it \Delta_x}\cdot\frac{8 \hspace{0.05cm}\sigma_2}{\it \Delta_y}= N_2 \cdot \sigma_1 \cdot \sigma_2 .$$

The quotient is thus with $\sigma_1^2 = \lambda_1$ and $\sigma_2^2 = \lambda_2$:

$${N_2\hspace{0.01cm}'}/{N_2} = \sigma_1 \cdot \sigma_2 = \sqrt{{4}/{3}} \cdot \sqrt{{2}/{3}} = \frac{2 \cdot \sqrt{2}}{3} \hspace{0.15cm}\underline{ \approx 0.943}.$$

(3) The equation of determination of the eigenvalues of $\mathbf{K_z}$ is:

$${\rm det} \left[ \begin{array}{ccc} 1-\lambda & 1/3 & 1/3\\ 1/3 & 1-\lambda & 1/3\\ 1/3 & 1/3 & 1-\lambda \end{array}\right] = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}(1- \lambda) \left[(1- \lambda)^2 - \frac{1}{9} \right]- \frac{1}{3} \left[\frac{1}{3}(1- \lambda) - \frac{1}{9} \right] + \frac{1}{3} \left[\frac{1}{9} - \frac{1}{3}(1- \lambda) \right] = 0$$

$$\Rightarrow \hspace{0.3cm}(1- \lambda) (\lambda^2 -2\lambda+ \frac{8}{9})- \frac{1}{9} (\frac{2}{3}- \lambda )+ \frac{1}{9} ( \lambda - \frac{2}{3})= 0$$

$$\Rightarrow \hspace{0.3cm}\lambda^2 - 2\lambda + \frac{8}{9} - \lambda^3 + 2 \lambda^2 - \frac{8}{9}\lambda - \frac{4}{27} + \frac{2}{9}\lambda = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\lambda^3 - 3 \lambda^2 + \frac{24}{9}\lambda - \frac{20}{27} = 0.$$

This equation has already been given as a solution hint, as well as one of the solutions: $\lambda_1= 5/3$.
This gives the equation for the further eigenvalues $\lambda_2$ and $\lambda_3$ to

$$\frac{\lambda^3 - 3 \lambda^2 + {24}/{9}\lambda - {20}/{27}}{\lambda -{5}/{3}} = \lambda^2 - {4}/{3} \cdot \lambda + {4}/{9} =0.$$

This equation can be transformed as follows: $(\lambda - {2}/{3})^2 =0.$

The other eigenvalues besides $\lambda_1= 5/3$ are thus equal and result in $\lambda_2 = \lambda_3 =2/3\hspace{0.15cm}\underline{=0.667}$.

(4) Analogous to the procedure in the subtask (2) results here:

$${N_3\hspace{0.01cm}'}/{N_3} = \sqrt{\lambda_1 \cdot \lambda_2\cdot \lambda_3} = \sqrt{\frac{5}{3} \cdot \frac{2}{3}\cdot \frac{2}{3}} = \sqrt{\frac{20}{27}} \hspace{0.15cm}\underline{ \approx 0.861}.$$