Exercise 4.2: Triangular PDF

Two triangular PDFs

Two probability density functions $\rm (PDF)$ with triangular shapes are considered.

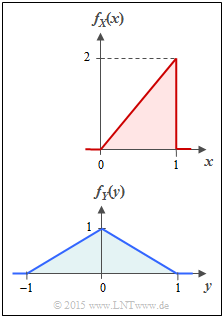
The random variable $X$ is limited to the range from $0$ to $1$ , and it holds for the PDF (upper sketch):

$f_X(x) = \left\{ \begin{array}{c} 2x \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm} 0 \le x \le 1 \\ {\rm else} \\ \end{array} \hspace{0.05cm}.$

According to the lower sketch, the random variable $Y$ has the following PDF:

$f_Y(y) = \left\{ \begin{array}{c} 1 - |\hspace{0.03cm}y\hspace{0.03cm}| \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm} |\hspace{0.03cm}y\hspace{0.03cm}| \le 1 \\ {\rm else} \\ \end{array} \hspace{0.05cm}.$

For both random variables, the differential entropy is to be determined in each case.

For example, the corresponding equation for the random variable $X$ is:

$h(X) = \hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{{\rm supp}\hspace{0.03cm}(\hspace{-0.03cm}f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \big [ f_X(x) \big ] \hspace{0.1cm}{\rm d}x \hspace{0.6cm}{\rm with}\hspace{0.6cm} {\rm supp}(f_X) = \{ x\text{:} \ f_X(x) > 0 \} \hspace{0.05cm}.$

If the "natural logarithm", the pseudo-unit "nat" must be added.
If, on the other hand, the result is asked in "bit" then the "dual logarithm" ⇒ " $\log_2$ " is to be used.

In the fourth subtask, the new random variable $Z = A \cdot Y$ is considered. Here, the PDF parameter $A$ is to be determined in such a way that the differential entropy of the new random variable $Z$ yields exactly $1$ bit :

$h(Z) = h (A \cdot Y) = h (Y) + {\rm log}_2 \hspace{0.1cm} (A) = 1\ {\rm bit} \hspace{0.05cm}.$

Hints:

The task belongs to the chapter Differential Entropy.
Useful hints for solving this task and further information on continuous random variables can be found in the third chapter "Continuous Random Variables" of the book Theory of Stochastic Signals.

Given the following indefinite integral:

$\int \xi \cdot {\rm ln} \hspace{0.1cm} (\xi)\hspace{0.1cm}{\rm d}\xi = \xi^2 \cdot \big [1/2 \cdot {{\rm ln} \hspace{0.1cm} (\xi)} - {1}/{4}\big ] \hspace{0.05cm}.$

Questions

Solution

(1) For the probability density function, in the range

$0 \le X \le 1$ , it is agreed that:

$f_X(x) = 2x = C \cdot x \hspace{0.05cm}.$

Here we have replaced "2" by $C$ ⇒ generalization in order to be able to use the following calculation again in subtask $(3)$ .

Since the differential entropy is sought in "nat", we use the natural logarithm. With the substitution $\xi = C \cdot x$ we obtain:

$h_{\rm nat}(X) = \hspace{0.1cm} - \int_{0}^{1} \hspace{0.1cm} C \cdot x \cdot {\rm ln} \hspace{0.1cm} \big[ C \cdot x \big] \hspace{0.1cm}{\rm d}x = \hspace{0.1cm} - \hspace{0.1cm}\frac{1}{C} \cdot \int_{0}^{C} \hspace{0.1cm} \xi \cdot {\rm ln} \hspace{0.1cm} [ \xi ] \hspace{0.1cm}{\rm d}\xi = - \hspace{0.1cm}\frac{\xi^2}{C} \cdot \left [ \frac{{\rm ln} \hspace{0.1cm} (\xi)}{2} - \frac{1}{4}\right ]_{\xi = 0}^{\xi = C} \hspace{0.05cm}$

Here the indefinite integral given in the front was used. After inserting the limits, considering $C=2$ , we obtain::

$h_{\rm nat}(X) = - C/2 \cdot \big [ {\rm ln} \hspace{0.1cm} (C) - 1/2 \big ] = - {\rm ln} \hspace{0.1cm} (2) + 1/2 = - {\rm ln} \hspace{0.1cm} (2) + 1/2 \cdot {\rm ln} \hspace{0.1cm} ({\rm e}) = {\rm ln} \hspace{0.1cm} (\sqrt{\rm e}/2)\hspace{0.05cm} = - 0.193 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} h(X) \hspace{0.15cm}\underline {= - 0.193\,{\rm nat}} \hspace{0.05cm}.$

(2) In general:

To calculate

$h(Y)$

$h_{\rm bit}(X) = \frac{h_{\rm nat}(X)}{{\rm ln} \hspace{0.1cm} (2)\,{\rm nat/bit}} = - 0.279 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} h(X) \hspace{0.15cm}\underline {= - 0.279\,{\rm bit}} \hspace{0.05cm}.$

You can save this conversion if you directly replace $(1)$ direct "ln" by "log₂" already in the analytical result of subtask:

$h(X) = \ {\rm log}_2 \hspace{0.1cm} (\sqrt{\rm e}/2)\hspace{0.05cm}, \hspace{1.3cm} {\rm pseudo-unit\hspace{-0.1cm}:\hspace{0.15cm} bit} \hspace{0.05cm}.$

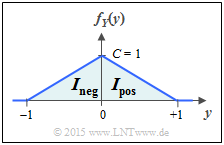
(3) We again use the natural logarithm and divide the integral into two partial integrals:

$h(Y) = \hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{{\rm supp} \hspace{0.03cm}( \hspace{-0.03cm}f_Y)} \hspace{-0.35cm} f_Y(y) \cdot {\rm ln} \hspace{0.1cm} \big[ f_Y(y) \big] \hspace{0.1cm}{\rm d}y = I_{\rm neg} + I_{\rm pos} \hspace{0.05cm}.$

The first integral for the range $-1 \le y \le 0$ is identical in form to that of subtask $(1)$ and only shifted with respect to it, which does not affect the result.
Now the height $C = 1$ instead of $C = 2$ has to be considered:

$I_{\rm neg} =- C/2 \cdot \big [ {\rm ln} \hspace{0.1cm} (C) - 1/2 \big ] = -1/2 \cdot \big [ {\rm ln} \hspace{0.1cm} (1) - 1/2 \cdot {\rm ln} \hspace{0.1cm} ({\rm e}) \big ]= 1/4 \cdot {\rm ln} \hspace{0.1cm} ({\rm e}) \hspace{0.05cm}.$

The second integrand is identical to the first except for a shift and reflection. Moreover, the integration intervals do not overlap ⇒ $I_{\rm pos} = I_{\rm neg}$ :

$h_{\rm nat}(Y) = 2 \cdot I_{\rm neg} = 1/2 \cdot {\rm ln} \hspace{0.1cm} ({\rm e}) = {\rm ln} \hspace{0.1cm} (\sqrt{\rm e}) \hspace{0.3cm} \Rightarrow\hspace{0.3cm}h_{\rm bit}(Y) = {\rm log}_2 \hspace{0.1cm} (\sqrt{\rm e}) \hspace{0.3cm} \Rightarrow\hspace{0.3cm} h(Y) = {\rm log}_2 \hspace{0.1cm} (1.649)\hspace{0.15cm}\underline {= 0.721\,{\rm bit}}\hspace{0.05cm}.$

(4) For the differential entropy of the random variable $Z = A \cdot Y$ holds in general:

$h(Z) = h(A \cdot Y) = h(Y) + {\rm log}_2 \hspace{0.1cm} (A) \hspace{0.05cm}.$

Thus, from the requiremen $h(Z) = 1 \ \rm bit$ and the result of subtask $(3)$ follows:

${\rm log}_2 \hspace{0.1cm} (A) = 1\,{\rm bit} - 0.721 \,{\rm bit} = 0.279 \,{\rm bit} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} A = 2^{0.279}\hspace{0.15cm}\underline {= 1.213} \hspace{0.05cm}.$