Exercise 4.2Z: About the Sampling Theorem
The sampling theorem states that the sampling frequency $f_{\rm A} = 1/T_{\rm A}$ must be at least twice as large as the largest frequency $f_\text {N, max}$ contained in the source signal $q(t)$:
- $$f_{\rm A} \ge 2 \cdot f_{\rm N,\hspace{0.05cm}max}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} T_{\rm A} \le \frac{1}{2 \cdot f_{\rm N, \hspace{0.05cm}max}}\hspace{0.05cm}.$$
If this condition is met, then at the receiver the message signal can be passed through a rectangular (ideal) low-pass filter with frequency response
- $$H(f) = \left\{ \begin{array}{l} 1 \\ 1/2 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{10}c} {\hspace{0.04cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| < f_{\rm G},} \\ {\hspace{0.04cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| = f_{\rm G},} \\ {\hspace{0.04cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| > f_{\rm G}} \\ \end{array}$$
can be completely reconstructed, that is, it is then $v(t) = q(t)$.
- The cutoff frequency $f_{\rm G}$ is to be chosen equal to half the sampling frequency.
- The equal sign is generally valid only if the spectrum $Q(f)$ does not contain a discrete spectral line at frequency $f_\text {N, max}$.
In this exercise, three different source signals are considered, each of which can be expressed as a harmonic oscillation
- $$q(t) = A \cdot \cos (2 \pi \cdot f_{\rm N} \cdot t - \varphi)$$
with amplitude $A = 1\ \rm V$ and frequency $f_{\rm N}= 5 \ \rm kHz$. For the spectral function $Q(f)$ of all represented time signals generally holds:
- $$Q(f) = \frac{A}{2} \cdot \delta (f- f_{\rm N}) \cdot {\rm e}^{-{\rm j}\hspace{0.04cm}\cdot \hspace{0.04cm}\varphi}+ \frac{A}{2} \cdot \delta (f+ f_{\rm N}) \cdot {\rm e}^{+{\rm j}\hspace{0.04cm}\cdot \hspace{0.04cm}\varphi}\hspace{0.05cm}.$$
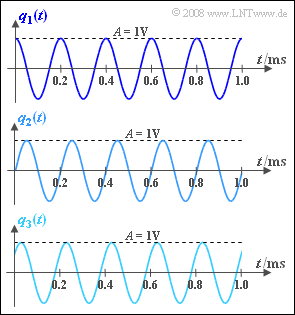
The oscillations sketched in the graph differ only by the phase $φ$:
- $φ_1 = 0$ ⇒ cosine signal $q_1(t)$,
- $φ_2 = π/2 \ (= 90^\circ)$ ⇒ sinusoidal signal $q_2(t)$,
- $φ_3 = π/4 \ (= 45^\circ)$ ⇒ signal $q_3(t)$.
Hints:
- The exercise belongs to the chapter "Pulse Code Modulation".
- Reference is made in particular to the page "Sampling and Signal Reconstruction".
- The sampled source signal is denoted by $q_{\rm A}(t)$ and its spectral function by $Q_{\rm A}(f)$.
- Sampling is always performed at $ν \cdot T_{\rm A}$.
Questions
Solution
- The sampling theorem is satisfied by $f_{\rm A} = 11 \ \rm kHz > 2 \cdot 5 \ \rm kHz$ so that a complete signal reconstruction is always possible.
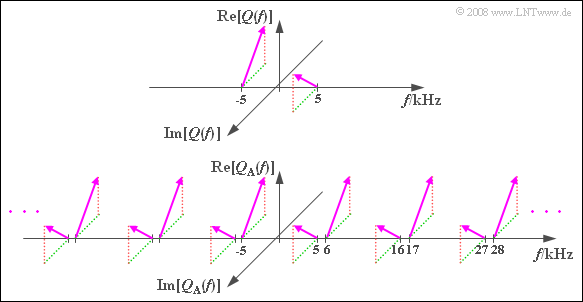
- The spectrum $Q_{\rm A}(f)$ results from $Q(f)$ by periodic continuation at the respective frequency spacing $f_{\rm A}$, which is generally illustrated in the graph.
- By a rectangular low-pass with $f_{\rm G} = f_{\rm A}/2 = 5.5 \ \rm kHz$ the original spectrum $Q(f)$ is obtained.
The shift by
- $f_{\rm A} = 11 \ \rm kHz$ yields the lines at $+6 \ \rm kHz$ and $+16 \ \rm kHz$,
- $-f_{\rm A} = -11 \ \rm kHz$ yields the lines at $-6 \ \rm kHz$ and $-16 \ \rm kHz$,
- $2 - f_{\rm A} = 22 \ \rm kHz$ yields the lines at $+17 \ \rm kHz$ and $+27 \ \rm kHz$,
- $-2 - f_{\rm A}= -22 \ \rm kHz$ yields the lines at $-17 \ \rm kHz$, $-27 \ \rm kHz$.
(2) The sampling distance is equal to the reciprocal of the sampling frequency:
- $$ T_{\rm A} = {1}/{f_{\rm A} }\hspace{0.15cm}\underline { = 0.1\,{\rm ms}} \hspace{0.05cm}.$$
(3) The correct solution is suggestion 2:
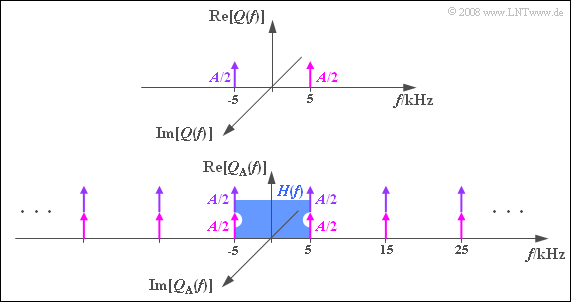
- For the cosinusoidal signal, according to this graph with $f_{\rm A} = 10 \rm \ kHz$: All spectral lines of $Q_{\rm A}(f)$: are real.
- The periodization of $Q(f)$ with $f_{\rm A} = 10 \rm \ kHz$ leads to a Dirac comb with spectral lines at $±f_{\rm N}$, $±f_{\rm N}± f_{\rm A}$, $±f_{\rm N}± 2f_{\rm A}$, . ..
- Through the superpositions, all Dirac functions have weight $A$, while the spectral lines of $Q(f)$ are weighted only by $A/2$ each.
- Because $H(f = f_{\rm N}) = H(f = f_{\rm G}) = 0.5$ the spectrum $V_1(f)$ after the low-pass is identical to $Q_1(f)$ ⇒ $v_1(t) = q_1(t)$.
- In the time domain, the signal reconstruction can be thought of as follows: The samples of $q_1(t)$ lie exactly at the signal maxima and minima.
- The lowpass filter forms the cosine signal with correct amplitude, frequency and phase.
(4) Correct is suggested solution 2:
- All sampled values of $q_2(t)$ now lie exactly at the zero crossings of the sinusoidal signal, which means that here $q_{\rm A}(t) \equiv 0$ holds. However, this naturally also gives $v_2(t) \equiv 0$.
- In the spectral domain, the result can be derived using the graph for subtask (1).
⇒ $Q(f)$ is purely imaginary and the imaginary parts at $±f_{\rm N}$ have different signs. - Thus, one positive and one negative part cancel each other in periodization
⇒ $Q_{\rm A}(f) \equiv 0$ ⇒ $V_2(f) \equiv 0$.
(5) None of the given solutions is correct:
- If in the graph for the subtask (1) the sampling frequency $f_{\rm A} = 11 \ \rm kHz$ is replaced by $f_{\rm A} = 10 \ \rm kHz$, the real parts add up, but the imaginary parts cancel out.
- This means that now $Q_{\rm A}(f)$ and $V_3(f)$ are real spectra. This further means:
- The phase information is lost $(φ = 0)$ and the output signal $v_3(t)$ is a cosine signal.
- $q_3(t)$ and $v_3(t)$ thus differ in both amplitude and phase. Only the frequency remains the same.
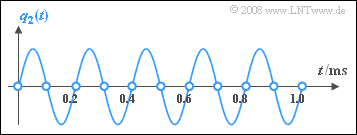
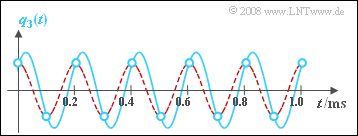
The graph shows
- turquoise the signal $q_3(t)$ and its samples (circles), and
- red dashed the output signal $v_3(t)$ of the low-pass.
You can see that the low-pass gives exactly the result you would probably choose if you were to draw a curve through the samples (circles).