Exercise 4.5Z: Tangent Hyperbolic and Inverse

• Return to book

$y = \tanh {(x)}$  tabularly

In the  "Theory Part"  it was shown,  using the example of a  "single parity–check code"  that the extrinsic  $L$ value with respect to the  $i^{th}$  symbol is defined as follows:

$$L_{\rm E}(i) = {\rm ln} \hspace{0.2cm}\frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} even} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} odd} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]} \hspace{0.05cm}.$$

• This equation is also applicable to many other channel codes.

• The code word  $\underline{x}^{(-i)}$  in this definition includes all symbols except  $x_i$  and has thus only length  $n-1$.

In the  $\text{Exercise 4.4}$  it was shown that the extrinsic  $L$ value can also be written as follows:

$$L_{\rm E}(i) = {\rm ln} \hspace{0.2cm} \frac{1 + \pi}{1 - \pi}\hspace{0.05cm}, \hspace{0.3cm} {\rm with} \hspace{0.3cm} \pi = \prod\limits_{j \ne i}^{n} \hspace{0.15cm}{\rm tanh}(L_j/2) \hspace{0.05cm}.$$

In this exercise,  we will now look for another calculation possibility.

Hints:

• This exercise belongs to the chapter  "Soft–in Soft–out Decoder".

• Reference is made in particular to the  "Calculations of extrinsic log likelihood ratios" section.

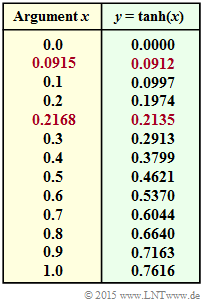
• Above you can see a table with the numerical values of the function  $y = \tanh(x)$   ⇒   "hyperbolic tangent".

• With the rows highlighted in red you can read the values of the inverse function  $x = \tanh^{-1}(y)$  needed for subtask  (5).

Questions

1

It holds   $\underline{L}_{\rm APP} = (+1.0, +0.4, -1.0)$.   Calculate the extrinsic  $L$ values   ⇒   $\underline{L}_{\rm E} = \big (L_{\rm E}(1), \ L_{\rm E}(2), \ L_{\rm E}(3) \big)$   according to the second equation given:

$L_{\rm E}(1) \ = \ $

$L_{\rm E}(2) \ = \ $

$L_{\rm E}(3) \ = \ $

2

Which of the properties does the function   $y = \tanh\hspace{-0.05cm}{(x)}$   exhibit?

	$\tanh\hspace{-0.05cm} {(x)} = ({\rm e}^x - {\rm e}^{-x}) \ / \ ({\rm e}^x + {\rm e}^{-x})$  is valid.
	$\tanh\hspace{-0.05cm} {(x)} = (1 - {\rm e}^{-2x}) \ / \ (1 + {\rm e}^{-2x})$  is valid.
	The function   $y = \tanh\hspace{-0.05cm} {(x)}$   is defined for all  $x$ values.
	$y_{\rm min} = 0$  and   $y_{\rm max} → ∞$  is valid.
	$y_{\rm min} = -1$  and   $y_{\rm max} = +1$   is valid.

3

What are the properties of the inverse function  $x = \tanh^{-1}\hspace{-0.08cm} {(y)}$?

	The function   $x = \tanh^{-1}\hspace{-0.05cm} (y)$   is defined for all  $y$  values.
	$x = \tanh^{-1}\hspace{-0.08cm} {(y)} = 1/2 \cdot \ln {[(1 + y) \ / \ (1 - y)]}$  is valid.
	$x_{\rm min} = -1$  and   $x_{\rm max} = +1$  is valid.
	$x_{\rm min} → -∞$  and   $x_{\rm max} → +∞$  is valid.

4

How can  $L_{\rm E}(i)$  also be represented?  Let  $\pi$  be defined as in the specification section.

	$L_{\rm E}(i) = \tanh^{-1}\hspace{-0.08cm} {(\pi)}$  is valid.
	$L_{\rm E}(i) = 2 \cdot \tanh^{-1}\hspace{-0.08cm} {(\pi)}$  is valid.
	$L_{\rm E}(i) = 2 \cdot \tanh^{-1}\hspace{-0.05cm}\big [ {\ln {[(1 + \pi) \ / \ (1 - \pi)]}}\big ]$  is valid.

5

Calculate the extrinsic  $L$ values using the equation given in exercise  (4).  Use the table in the information section for this purpose.

$L_{\rm E}(1) \ = \ $

$L_{\rm E}(2) \ = \ $

$L_{\rm E}(3) \ = \ $

Solution

Solution

(1)  According to the specification applies:

$$L_{\rm E}(i) = {\rm ln} \hspace{0.2cm} \frac{1 + \pi}{1 - \pi}\hspace{0.05cm}, \hspace{0.3cm} {\rm with} \hspace{0.3cm} \pi = \prod\limits_{j \ne i}^{3} \hspace{0.15cm}{\rm tanh}(L_j/2) \hspace{0.05cm}.$$

• From the table on the specification section can be read:

$$\tanh {(L_1/2)} = \tanh {(0.5)} = 0.4621,$$

$$\tanh {(L_2/2)} = \tanh {(0.2)} = 0.1974.$$

• Since the hyperbolic tangent is an odd function,  the following applies further

$$\tanh {(L_3/2)} = -\tanh {(0.5)} = -0.4621.$$

• Calculation of  $L_{\rm E}(1)$:

$$\pi = {\rm tanh}(L_2/2) \cdot {\rm tanh}(L_3/2) = (+0.1974) \cdot (-0.4621) = - 0.0912\hspace{0.3cm} \Rightarrow \hspace{0.3cm} L_{\rm E}(1) = {\rm ln} \hspace{0.2cm} \frac{1 -0.0912}{1 +0.0912}\hspace{0.15cm}\underline{=-0.1829} \hspace{0.05cm}.$$

• Calculation of  $L_{\rm E}(2)$:

$$\pi = {\rm tanh}(L_1/2) \cdot {\rm tanh}(L_3/2) = (+0.4621) \cdot (-0.4621) = - 0.2135\hspace{0.3cm} \Rightarrow \hspace{0.3cm} L_{\rm E}(2) = {\rm ln} \hspace{0.2cm} \frac{1 -0.2135}{1 +0.2135}\hspace{0.15cm}\underline{=-0.4337} \hspace{0.05cm}.$$

• Calculation of  $L_{\rm E}(3)$:

$$\pi = {\rm tanh}(L_1/2) \cdot {\rm tanh}(L_2/2) = (+0.4621) \cdot (+0.1974) = + 0.0912\hspace{0.3cm} \Rightarrow \hspace{0.3cm} L_{\rm E}(3) = {\rm ln} \hspace{0.2cm} \frac{1 +0.0912}{1 -0.0912}\hspace{0.15cm}\underline{=+0.1829}= - L_{\rm E}(1) \hspace{0.05cm}.$$

(2) Correct are the  solutions 1, 2, 3, and 5:  The function

$$y ={\rm tanh}(x) = \frac{{\rm e}^{x}-{\rm e}^{-x}}{{\rm e}^{x}+{\rm e}^{-x}} = \frac{1-{\rm e}^{-2x}}{1+{\rm e}^{-2x}}$$

is computable for all  $x$  values and   $\tanh(-x) = -\tanh(x)$  holds.

• For large values of  $x$:     ${\rm e}^{-2x}$  becomes very small,  so that in the limiting case   $x → ∞$  the limit  $y = 1$  is obtained.

(3)  Since the  "hyperbolic tangent"  only yields values between  $±1$,  the inverse function   $x = \tanh^{-1}(y)$   can also only be evaluated for  $|y| ≤ 1$.

• By rearranging the given equation

$$x ={\rm tanh}^{-1}(y) = 1/2 \cdot {\rm ln} \hspace{0.2cm} \frac{1+y}{1-y}$$

one obtains:

$${\rm e}^{2x} = \frac{1+y}{1-y} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\rm e}^{-2x} = \frac{1-y}{1+y} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} (1+y) \cdot {\rm e}^{-2x} = 1-y \hspace{0.3cm} \Rightarrow \hspace{0.3cm}y = \frac{1-{\rm e}^{-2x}}{1+{\rm e}^{-2x}} = {\rm tanh}(x) \hspace{0.05cm}.$$

• This means:

1. The equation given in the  proposed solution 2  is correct.
2. In the limiting case  $y → 1$,   $x = \tanh^{-1}(y) → ∞$  holds.
3. Also the inverse function is odd   ⇒   in the limiting case  $y → -1$  goes  $x → -∞$.

• Accordingly,  the  proposed solutions 2 and 4  are correct.

(4)  Starting from the equation.

$$L_{\rm E}(i) = {\rm ln} \hspace{0.2cm} \frac{1 + \pi}{1 - \pi}$$

one arrives with the result of  (3)  at the equivalent equation corresponding to  proposed solution 2:

$$L_{\rm E}(i) = 2 \cdot {\rm tanh}^{-1}(\pi)\hspace{0.05cm}.$$

(5)  With the result of the subtask  (1)  we get

• for the first extrinsic  $L$  value,  since  $\pi_1 = -0.0912$:

$$L_{\rm E}(1) = 2 \cdot {\rm tanh}^{-1}(-0.0912)= -2 \cdot {\rm tanh}^{-1}(0.0912) = -2 \cdot 0.0915\hspace{0.15cm}\underline{=-0.1830} \hspace{0.05cm}.$$

• for the second extrinsic  $L$  value,  since  $\pi_2 = -0.2135$:

$$L_{\rm E}(2) = -2 \cdot {\rm tanh}^{-1}(0.2135) = -2 \cdot 0.2168\hspace{0.15cm}\underline{=-0.4336} \hspace{0.05cm}.$$

• for the third extrinsic  $L$ value,  since  $\pi_3 = +0.0912 = -\pi_1$:

$$L_{\rm E}(3) = -L_{\rm E}(1) \hspace{0.15cm}\underline{=+0.1830} \hspace{0.05cm}.$$

Note:

• The result was determined using the red table entries on the information section.

• Except for rounding errors  $($multiplication/division by  $2)$,  the result agrees with the results of subtask  (1).