Exercise 4.7Z: Generation of a Joint PDF

• Return to book

Requirements for the generation of a
two-dimensional random variable

Given statistically independent quantities  $u$  and  $v$,

• both of which are uniformly distributed between  $-1$  and  $+1$,  and
• thus each have variance  $\sigma^2 = 2/3$, 

generate a two-dimensional random variable  $(x,\hspace{0.08cm} y)$  where for the components:

$$x = A \cdot u + B \cdot v + C,$$

$$y= D \cdot u + E \cdot v + F.$$

The two-dimensional random variable  $(x,\hspace{0.08cm} y)$  to be generated should have the following statistical properties:

• Let the variances be  $\sigma_x^2 = 4$  and  $\sigma_y^2 = 10$.
• Let the random variable  $x$  be mean-free  $(m_x =0)$.
• For the mean of  $y$  let  $m_y = 1$  hold.
• The correlation coefficient between  $x$  and  $y$  is  $\rho_{xy} = \sqrt{0.9} = 0.949.$
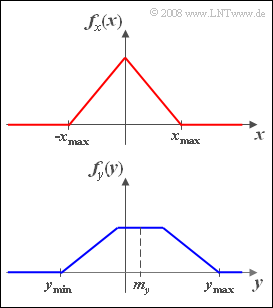
• The random variable  $x$  possess a triangular PDF $f_x(x)$  corresponding to the above graph.
• The random variable  $y$  has a trapezoidal PDF $f_y(y)$  according to the lower graph.

Hints:

• The exercise belongs to the chapter  Linear Combinations of Random Variables.
• In particular,  reference is made to the page  Generation of correlated random variables.
• To avoid ambiguity,  it is specified that all coefficients  $A$, ... , $F$  should be non-negative.

Questions

1

Determine the coefficients  $C$  and  $F$.

$C \ = \ $

$F\ = \ $

2

Determine the coefficients  $A$  and  $B$.

$A \ = \ $

$B \ = \ $

3

Determine the coefficients  $D$  and  $E$,  where  $D > E$  should hold.

$D \ = \ $

$E \ = \ $

4

Specify the maximum values for  $x$  and  $y$.

$x_\text{max}\ = \ $

$y_\text{max}\ = \ $

Solution

Solution

(1)  Given the mean values,  it must hold:

$$ C = m_x\hspace{0.15cm}\underline{ = 0},$$

$$ F = m_y\hspace{0.15cm}\underline{ = 1}.$$

(2)  Taking into account  $\sigma^2 = 2/3$  holds:

$$\sigma_x^2 = \sigma^2 \cdot ( A^2 + B^2)= {2}/{3} \cdot ( A^2 + B^2) .$$

• Because of  $\sigma_x^2 = 4$  it follows  $A^2 + B^2= 6$.
• A triangular PDF means that  $A = \pm B$  must hold.
• Thus,  since negative coefficients have been excluded,  we obtain:

$$ A = B = \sqrt{3}\hspace{0.15cm}\underline{ = 1.732}.$$

Rhombic joint PDF

(3)  With  $ A = B = \sqrt{3}$  corresponding to the last subtask,  two equations of determination remain for  $D$  and  $E$:

$$\sigma_y^2 = \sigma^2 \cdot ( D^2 + E^2)= 10 \hspace{0.5cm} \Rightarrow \hspace{0.5cm} D^2 + E^2 = \frac {\sigma_y^2}{\sigma^2} = \frac {10}{2/3} \stackrel{!}{=}15,$$

$$\rho_{xy} = \frac{A \cdot D + B \cdot E}{\sqrt{(A^2 + B^2)(D^2 + E^2)}} = \frac{\sqrt{3} \cdot (D + E)}{\sqrt{6 \cdot (D^2 + E^2)}} \stackrel{!}{=} \sqrt{0.9}.$$

• From this it further follows:  $D + E = \sqrt{1.8 \cdot ( D^2 + E^2)} = \sqrt{27} = 3 \cdot \sqrt{3}.$
• The equation,  in conjunction with  $D^2 + E^2 = 15$  and the constraint  $(D>E)$  leads to the result:

$$ D= 2 \cdot \sqrt{3}\hspace{0.15cm}\underline{ = 3.464}, \hspace{0.5cm}E= \sqrt{3} \hspace{0.15cm}\underline{= 1.732}.$$

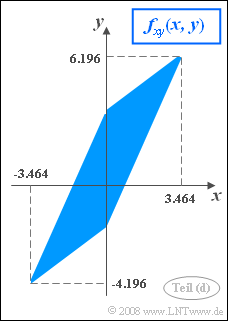
(4)  The random variables  $x$  and  $y$  resp. take their maximum values when  $u= +1$ and  $v= +1$  holds:

$$ x_\text{max}= A+B \hspace{0.15cm}\underline{ = +3.464}, \hspace{0.5cm} x_\text{min} = - A - B= -3.464.$$

$$ y_\text{max}= D+E+F \hspace{0.15cm}\underline{ = +6.196}, \hspace{0.5cm} y_\text{min} = -D-E+F= -4.196.$$