Exercise 5.1Z: Cosine Square Noise Limitation

Top: Input PSD ${\it Φ}_x(f)$, Bottom: Frequency response $H(f)$

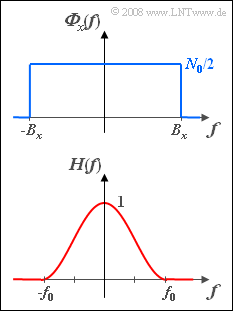
We consider bandlimited white noise $x(t)$ with the power-spectral density ${\it Φ}_x(f)$ sketched above. This is constant equal to $N_0/2$ in the range $|f| \le B_x$ and zero outside.

Assume the following numerical values:

Noise power-spectral density $N_0 = 10^{-16} \ \rm V^2/Hz$,
(one-sided) noise bandwidth $B_x = 10 \ \rm kHz$.

This signal is applied to the input of a low-pass filter with frequency response

$$H(f) = \left\{ {\begin{array}{*{20}c} {\cos ^2 \left( {\frac{{{\rm{\pi }}f}}{2f_0 }} \right)} & {\rm{f\ddot{u}r}\quad \left| \it f \right| \le \it f_{\rm 0} ,} \\ 0 & {{\rm{else}}} \\\end{array}} \right.$$

Here, $f_0$ denotes the absolute filter bandwidth, which can vary between $B_x/2$ and $2B_x$.

The filter output signal is denoted by $y(t)$.

Notes:

The exercise belongs to the chapter Stochastic System Theory.
Reference is also made to the chapters Gaussian Distributed Random Variables and Power-Spectral Density.

Use the following equations if necessary:

$${\rm Q}(x) \approx \frac{1}{{\sqrt {2{\rm{\pi }}} \cdot x}} \cdot {\rm{e}}^{ - x^2 /2} \hspace{0.15cm}( \text{for large }x),$$

$$\int {\rm{cos}}^{\rm{2}}( {ax} )\hspace{0.1cm}{\rm{d}}x = \frac{1}{2} \cdot x + \frac{1}{4a} \cdot \sin ( {2ax} ),$$

$$\int {\cos ^4 } ( {ax} )\hspace{0.1cm}{\rm{d}}x = \frac{3}{8} \cdot x + \frac{1}{4a} \cdot \sin ( {2ax} ) + \frac{1}{32a} \cdot \sin ( {4ax} ).$$

Questions

$\sigma_x \ = \ $

$\ \rm µ V$

${\rm Pr}(|x(t)| > 5 \hspace{0.05cm} \rm µ V) \ = \ $

$\ \cdot 10^{-6}$

$m_y\ \ = \ $

$\ \rm µ V$

$\sigma_y \ = \ $

$\ \rm µ V$

$\sigma_y \ = \ $

$\ \rm µ V$

${\rm Pr}(|y(t)| > 5 \hspace{0.05cm} \rm µ V) \ = \ $

$\ \cdot 10^{-12}$

Solution

(1) The variance of the signal $x(t)$ is

$$\sigma _x ^2 = \frac{N_0 }{2} \cdot 2B_x = N_0 \cdot B_x = 10^{ - 12} \;{\rm{V}}^2 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} \sigma _x \hspace{0.15cm}\underline{ = 1\,\,{\rm µ}{\rm V}}.$$

(2) According to the chapter "Gaussian Distributed Random Variables" and the approximation given here $($for large $x)$, we obtain:

$$\Pr \left( {\left| {x(t)} \right| > 5\;{\rm{µ V}}} \right) = 2 \cdot {\rm Q}(5) = \frac{2}{{\sqrt {2{\rm{\pi }}} \cdot 5}} \cdot {\rm{e}}^{ - 12.5}\hspace{0.15cm} \underline{ \approx 0.6 \cdot 10^{ - 6}} .$$

(3) The input signal $x(t)$ is mean-free ⇒ $m_x = 0$.

Otherwise ${\it Φ}_x(f)$ would still have to contain a Dirac delta function at $f= 0$.
The mean is not changed by the linear filter ⇒ $m_y\hspace{0.05cm}\underline{ = 0}$.

(4) For the power-spectral density of the output signal generally applies:

$${\it \Phi}_y (f) = {N_0 }/{2} \cdot \left| {H( f )} \right|^2 .$$

Thus, the variance $\sigma _y^2$ can be calculated. Taking advantage of the symmetry, we obtain:

$$\sigma _y ^2 = {N_0 }/{2} \cdot \int_{ - \infty }^{ + \infty } {\left| {H( f )} \right|^2 \hspace{0.1cm}{\rm{d}}f} = N_0 \cdot \int_0^{f_0 } {\cos ^4 } \left( {\frac{{{\rm{\pi }}f}}{2f_0 }} \right)\hspace{0.1cm}{\rm{d}}f .$$

The definite integral is given. For each of the three solution terms, the value of the lower bound is zero. It follows that:

$$\sigma _y ^2 = {N_0}/{2} \cdot \left( {\frac{3}{8} \cdot f_0 + \frac{f_0 }{{2{\rm{\pi }}}} \cdot \sin ( {\rm{\pi }} ) + \frac{f_0 }{{16{\rm{\pi }}}} \cdot \sin ( {{\rm{2\pi }}} )} \right) = \frac{3}{8} \cdot N_0 \cdot f_0 $$

$$\Rightarrow \hspace{0.3cm} f_0 = B_x/2\text{:}\hspace{0.2cm}\sigma _y ^2 = \frac{3}{16} \cdot N_0 \cdot B_x = \frac{3}{16} \cdot \sigma _x ^2 = 0.1875 \cdot 10^{ - 12} \;{\rm{V}}^2 \hspace{0.2cm}\Rightarrow \hspace{0.2cm}\sigma _y \hspace{0.15cm}\underline{ = 0.433\;{\rm{µ V}}}{\rm{.}}$$

(5) Now the input PSD for $|f| > B_x$ has no components.

Therefore holds:

$$\sigma _y ^2 = N_0\cdot \int_0^{B_x } {\cos ^4 \left( {\frac{{{\rm{\pi }}f}}{2f_0 }} \right)\hspace{0.1cm}{\rm{d}}f = N_0 \cdot \int_0^{f_0 /2} {\cos ^4 } \left( {\frac{{{\rm{\pi }}f}}{2f_0 }} \right)\hspace{0.1cm}{\rm{d}}f.}$$

The numerical evaluation yields for this:

$$\sigma _y ^2 = N_0 \left( {\frac{3}{8} \cdot B_x + \frac{B_x }{{2{\rm{\pi }}}} \cdot \sin ( {\frac{{\rm{\pi }}}{2}} ) + \frac{B_x }{{{\rm{16\pi }}}} \cdot \sin ( {\rm{\pi }} )} \right) = N_0 \cdot B_x \left( {\frac{3}{8} + \frac{1}{{2{\rm{\pi }}}}} \right) = 0.534\cdot \sigma _x ^2 \hspace{0.6cm}\Rightarrow \hspace{0.6cm}\sigma _y \hspace{0.15cm}\underline{ = 0.731\;{\rm{µ V}}}{\rm{.}}$$

(6) Analogous to the solution of subtask (2) holds:

$$\Pr \left( {\left| {y\left( t \right)} \right| > 5\;{\rm{µ V}}} \right) = 2 \cdot {\rm Q}\left( {\frac{{5\;{\rm{µ V}}}}{{0.731\;{\rm{µ V}}}}} \right) = 2 \cdot {\rm Q}( {6.84} ).$$

With the given approximation, this probability has the following value:

$$\Pr \left( {\left| {y\left( t \right)} \right| > 5\;{\rm{µ V}}} \right) \hspace{0.15cm} \underline{ \approx 8 \cdot 10^{ - 12}}.$$