Exercise 5.3: 1st order Digital Filter

First order digital filter

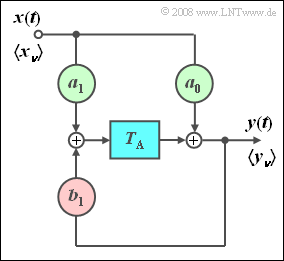
We consider the filter arrangement shown on the right with coefficients $a_0$, $a_1$ and $b_1$, each of which can take values between $0$ and $1$.

Let the input signal $x(t)$ be a single Dirac delta impulse with unit weight "1" ⇒ $x(t) = \delta(t)$, which corresponds to the following discrete-time representation:

$$\left\langle {\hspace{0.05cm}x_\nu } \hspace{0.05cm}\right\rangle = \left\langle \hspace{0.05cm}1,\;0,\;0,\;0,\;\text{...} \hspace{0.05cm}\right\rangle .$$

Due to this special input sequence, the sequence $\left\langle {\hspace{0.05cm}y_\nu \hspace{0.05cm}} \right\rangle$ at the filter output simultaneously describes the discrete-time impulse response $\left\langle {\hspace{0.05cm}h_\nu \hspace{0.05cm}} \right\rangle$ of the filter. The spacing of the samples here is $T_{\rm A} = 1 \hspace{0.05cm} \rm µ s$.

Note:

The exercise belongs to the chapter Digital Filters.
The HTML5/JavaScript applet "Digital Filters" illustrates the subject matter of this chapter.

Questions

	The special case $b_1 = 1$ leads to a non-recursive filter.
	With $a_0 = 1$, $a_1 = 0$ and $b_1 = 0$: $y(t) = x(t)$ is true.
	With $a_0 = 0$, $a_1 = 0.5$ and $b_1 = 0$: $y(t)$ is undistorted with respect to $x(t)$.

$y_3 \ = \ $

$M \ = \ $

$y_3 \ = \ $

Solution

(1) Solutions 2 and 3 are correct:

The filter is non-recursive if the feedback is omitted: $b_1 = 0$.
If additionally $a_0 = 1$ and $a_1 = 0$, the sequences $\left\langle {x_\nu } \right\rangle$ and $\left\langle {y_\nu } \right\rangle$ and thus of course the signals $x(t)$ and $y(t)$ are equal.
With $a_0 = 0$ and $a_1 = 1$, $y(t) = x(t-T_{\rm A})$ is delayed by $T_{\rm A}$ with $a_1 = 0.5$ additionally attenuated.
However, delay and damping do not result in distortion.

(2) At time $\nu = 0$: $y_{\nu} = x_{\nu} = 1$.

For all further time points: $\nu$, $x_{\nu} = 0$ and thus:

$$y_\nu = b_1 \cdot y_{\nu - 1} = {b_1 }^\nu .$$

In particular, $y_3 = b_1^3 = 0.6^3\hspace{0.15cm}\underline{= 0.216}$.

(3) According to the problem definition must be valid:

$$y_{M + 1} = {b_1} ^{M + 1} < 0.001.$$

This leads to the result:

$$M + 1 \ge \frac{{\lg \ \left( {0.001} \right)}}{{\lg \ \left( {0.6} \right)}} = \frac{ - 3}{ - 0.222} \approx 13.51\quad \Rightarrow \quad \hspace{0.15cm} \underline{M = 13}.$$

Checking the values of $y_{13} \approx 0.0013$ and $y_{14} \approx 0.0008$ confirms this result.

(4) Due to the linearity of the present filter, the same result is obtained

if the filter is not changed compared to subtask (2) $(a_1 = 0)$
and the input sequence $\left\langle {x_\nu } \right\rangle = \left\langle {1,\; - 0.5,\;0,\;0,\;\text{...} } \right\rangle$ is considered.

One then obtains in general for $\nu \gt 0$:

$$y_\nu = {b_1} ^\nu + a_1 \cdot {b_1} ^{\nu - 1} = \left( {b_1 + a_1 } \right) \cdot {b_1} ^{\nu - 1} .$$

With $b_1 = 0.6$ and $a_1 = -0.5$, this gives $y_\nu = 0.1\cdot {0.6} ^{\nu - 1}$, and thus the sequence $\left\langle {y_\nu } \right\rangle = \left\langle {1,\;0.1,\;0.06,\;0.036,\;\text{...} } \right\rangle .$

The value we are looking for is $y_3\hspace{0.15cm}\underline{= 0.036}$.