Exercise 5.4: Sine Wave Generator

Proposed filter structure

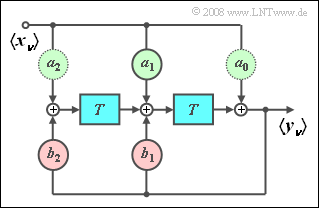
The diagram shows a second-order digital filter suitable for generating a discrete-time sinusoidal function on a digital signal processor $\rm (DSP)$, for example:

$$\left\langle \hspace{0.05cm}{y_\nu }\hspace{0.05cm} \right\rangle = \left\langle {\, \sin ( {\nu T \cdot \omega _0 } )\, }\right\rangle .$$

It is assumed that the input sequence $\left\langle \hspace{0.05cm} {x_\nu } \hspace{0.05cm}\right\rangle$ describes a (discrete-time) Dirac delta function. Thus, all output values $y_\nu$ are simultaneously identical to zero for times $\nu\lt 0$.
The total of five filter coefficients result from the $Z$-transform:

$$Z \{ {\sin ( {\nu T \omega _0 } )} \} = \frac{{z \cdot \sin \left( {\omega _0 T} \right)}}{{z^2 - 2 \cdot z \cdot \cos \left( {\omega _0 T} \right) + 1}}.$$

Substituting this equation by a recursive second order filter $(M = 2)$, we obtain the following filter coefficients:

$$a_0 = 0,\quad a_1 = \sin \left( {\omega _0 T} \right),\quad a_2 = 0, \quad b_1 = 2 \cdot \cos \left( {\omega _0 T} \right),\quad b_2 = - 1.$$

In the diagram it is already marked by the lighter border that the filter coefficients $a_0$ and $a_2$ can be omitted.

Notes:

The exercise belongs to the chapter Digital Filters in this book.
The HTML5/JavaScript applet "Digital Filters" illustrates the subject matter of this chapter.
For the subtasks (1) to (3) the following apply:

$$a_1 = 0.5,\quad b_1 = \sqrt 3 .$$

Questions

$y_0 \ = \ $

$y_1 \ = \ $

$y_2 \ = \ $

$y_7 \ = \ $

$T_0/T\ = \ $

$a_1 \ = \ $

$b_1 \ = \ $

Solution

(1) The "$1$" at the input affects $($because of $a_0= 0)$ at the output only at the time $\nu = 1$:

$$y_0 \hspace{0.15cm} \underline{= 0},\quad y_1 \hspace{0.15cm} \underline{ = 0.5}.$$

At $\nu = 2$, the recursive part of the filter also takes effect:

$$y_2 = b_1 \cdot y_1 - y_0 = {\sqrt 3 }/{2} \hspace{0.15cm} \underline{ \approx 0.866}.$$

(2) For $\nu \ge 2$, the filter is purely recursive:

$$y_\nu = b_1 \cdot y_{\nu - 1} - y_{\nu - 2} .$$

In particular, one obtains

$$y_3 = \sqrt 3 \cdot y_2 - y_1 = \sqrt 3 \cdot {\sqrt 3 }/{2} - {1}/{2} = 1;$$

$$y_4 = \sqrt 3 \cdot y_3 - y_2 = \sqrt 3 \cdot 1 - {\sqrt 3 }/{2} = {\sqrt 3 }/{2};$$

$$y_5 = \sqrt 3 \cdot y_4 - y_3 = \sqrt 3 \cdot {\sqrt 3 }/{2} - 1 = {1}/{2};$$

$$y_6 = \sqrt 3 \cdot y_5 - y_4 = \sqrt 3 \cdot {1}/{2} - {\sqrt 3 }/{2} = 0;$$

$$y_7 = \sqrt 3 \cdot y_6 - y_5 = \sqrt 3 \cdot 0 - {1}/{2} \hspace{0.15cm} \underline{= - 0.5}.$$

(3) By continuing the recursive algorithm of subtask (2), we obtain for large $\nu$–values:

$$y_\nu = y_{\nu - 12} .$$

From this follows $T_0/T\hspace{0.15cm} \underline{= 12}$. The same result is obtained by the following considerations:

$$a_1 = \sin \left( {\omega _0 \cdot T} \right) = \sin \left( {2{\rm{\pi }}\cdot{T}/{T_0 }} \right)\mathop = \limits^! {1}/{2} = \sin \left( {{{\rm{\pi }}}/{6}} \right) \;\;{\rm \Rightarrow} \;\;{2T}/{T_0 } = {1}/{6}\quad \Rightarrow \;\;{T_0 }/{T} = 12.$$

Checking the coefficient $b_1$ confirms the calculation:

$$b_1 = 2 \cdot \cos \left( {{{\rm{\pi }}}/{6}} \right) = 2 \cdot {\sqrt 3 }/{2} = \sqrt 3 .$$

(4) From $f_0 = 10 \hspace{0.15cm} \rm kHz$ follows $T_0 = 100 \hspace{0.05cm} \rm µ s$ or $T_0/T = 100$ . This gives:

$$a_1 = \sin \left( {2{\rm{\pi }}\cdot{T}/{T_0 }} \right) = \sin \left( {3.6^ \circ } \right) \hspace{0.15cm} \underline{\approx 0.062},$$

$$b_1 = 2 \cdot \cos \left( {2{\rm{\pi }}\cdot{T}/{T_0 }} \right) = 2 \cdot \cos \left( {3.6^ \circ } \right) \hspace{0.15cm} \underline{\approx 1.996}.$$