Exercise 5.5: ACF-equivalent Filters

Two ACF–equivalent filters

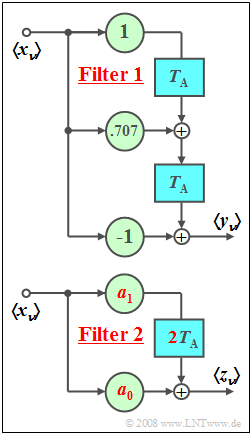
We consider the two digital filters outlined:

The individual elements of the input sequence $\left\langle {x_\nu } \right\rangle$ are in both cases statistically independent of each other and equally distributed between $-1$ and $+1$.
It follows directly for the mean and the variance:

$$m_x = 0,\quad \sigma _x^2 = {1}/{3}.$$

The delay times of $\text{Filter 1}$ are equal to $T_{\rm A} = 1 \hspace{0.05cm} \rm µ s$ in each case. The delays of $\text{Filter 2}$ are twice as long.

The coefficients $a_0$ and $a_1$ of $\text{Filter 2}$ should be set so that the auto-correlation functions $\rm (ACFs)$ of $\left\langle {y_\nu } \right\rangle$ and of $\left\langle {z_\nu } \right\rangle$ match exactly. If there are multiple solutions, please choose the one with $|a_1| < |a_0|$.

Notes:

The exercise belongs to the chapter Creation of Predefined ACF Properties.
The coefficients of $\text{Filter 1}$ are denoted by $\alpha_0$, $\alpha_1$, $\alpha_2$ ("alphas") in the questions.

Questions

	It is a non-recursive filter.
	The order of the filter is $M = 2$.
	The upper filter coefficient is equal to $\alpha_0 =+1$.

$\sigma_y \ = \ $

$\varphi_y(T_{\rm A}) \ = \ $

$\varphi_y(2T_{\rm A}) \ = \ $

$a_1/a_0 \ = \ $

	$f_y(y)$ and $f_z(z)$ are identical.
	$f_y(y)$ and $f_z(z)$ are different in general.
	With Gaussian input, $f_y(y)$ and $f_z(z)$ would be the same.

Solution

(1) The first two solutions are correct:

It is a second-order non-recursive filter with coefficients $\alpha_0 = -1$, $\alpha_1 = +0.707$ and $\alpha_2 = +1$.
The coefficients of $\text{Filter 1}$ are denoted here as $\alpha_0$, $\alpha_1$, $\alpha_2$ ("alphas").

(2) The variance of the output values is equal to the ACF value for $k = 0$. For this one obtains:

$$\varphi _y (0) = \sigma _x ^2 \cdot \left( {\alpha _0 ^2 + \alpha _1 ^2 + \alpha _2 ^2 } \right) = {1}/{3} \cdot \left( {1 + {1}/{2} + 1} \right) = 0.833.$$

This gives the standard deviation:

$$\sigma _y = \sqrt {\varphi _y (0)} \hspace{0.15cm} \underline{= 0.913}.$$

(3) These two ACF values can be calculated as follows:

$$\varphi _y ( {T_{\rm A} } ) = \sigma _x ^2 \cdot \left( {\alpha _0 \cdot \alpha _1 + \alpha _1 \cdot \alpha _2 } \right) = {1}/{3} \cdot \left( { - 1 \cdot 0.707 + 0.707 \cdot 1} \right) \hspace{0.15cm} \underline{= 0},$$

$$\varphi _y ( {2T_{\rm A} } ) = \sigma _x ^2 \cdot \left( {\alpha _0 \cdot \alpha _2 } \right) = -1/3\hspace{0.15cm} \underline{\approx - 0.333}.$$

(4) Because of $\varphi _y ( {T_{\rm A} } )= 0$, if $a_0$ and $a_1$ are chosen appropriately, it is possible that the ACF at the output of $\text{Filter 2}$ is identical to the ACF calculated in (3).

With $T_{\rm A}\hspace{0.05cm}' = 2 \cdot T_{\rm A}$ holds:

$$\varphi _z (0) = {1}/{3} \cdot \left( {a_0 ^2 + a_1 ^2 } \right) = 0.833\quad \Rightarrow \quad a_0 ^2 + a_1 ^2 = 2.5, $$

$$\varphi _z( {T_{\rm A} \hspace{0.05cm}'} ) = {1}/{3}\left( {a_0 \cdot a_1 } \right) = - {1}/{3}\quad \;\;\, \Rightarrow \quad a_0 \cdot a_1 = - 1.$$

With the auxiliary quantity $H = a_0^2$ this leads to the equation of determination:

$$H + {1}/{H} = 2.5\quad \Rightarrow \quad H^2 - 2.5 \cdot H + 1 = 0$$

$$\Rightarrow \hspace{0.3cm}H_{1/2} = {1}/{2} \cdot \left( {2.5 \pm \sqrt {2.5^2 - 4} } \right) = {1}/{2} \cdot \left( {2.5 \pm 1.5} \right).$$

The two solutions are $H_1 = 2$ and $H_2 = 1/2$. This gives four possible solutions:

$$a_0 = \sqrt 2 ,\quad \;\;\, a_1 = - {1}/{\sqrt 2 }, \hspace{2cm} a_0 = - \sqrt 2 ,\quad a_1 = {1}/{\sqrt 2 },$$

$$a_0 = {1}/{\sqrt 2 },\quad \;\,\, a_1 = - \sqrt 2 , \hspace{2cm} a_0 = - {1}/{\sqrt 2 },\quad a_1 = \sqrt 2 .$$

For the last two pairs of solutions, the condition $|a_1| < |a_0|$ is not satisfied. On the other hand, for the upper equations, in both cases:

$$ \hspace{0.15cm} \underline{a_1 /a_0 = - 0.5}.$$

(5) The solutions 2 and 3 are correct:

In general $($even with equally distributed input variable $x)$ the probability density functions $f_y(y)$ and $f_z(z)$ are different.
In this case, $f_z(z)$ results from the convolution of two rectangles of different width; thus, it is trapezoidal.
To calculate $f_y(y)$, on the other hand, three rectangles would have to be folded together.
With Gaussian input $x$: $y$ and $z$ are also Gaussian distributed, and because of $m_y = m_z$ and $\sigma_y = \sigma_z$, $f_z(z) = f_y(y)$ is also valid.